Considere o experimento aleatório onde um dado não viciado (equilibrado) é lançado e o valor da sua face é representado por . Considere a seguinte v.a.: . Defina a função de probabilidade acumulada, , com base na definição da v.a. , acima, e esboce o seu gráfico. Seja preciso tanto nos cálculos como no desenho.
Passo 1
Lendo tranquilamente o enunciado, conseguimos pegar rapidamente qual nosso experimento: lançar um dado, e olhar o valor da face (que ele chamou de )!
Nosso espaço amostral é dado por:
Passo 2
Já sabemos então que esse é justamente os valores que podem sair no lançamento de um dado, ou seja, um número de 1 até 6.
Além disso, ele dá pra gente uma variável aleatória , que é uma função de , e pede a FDA de . Para calcularmos , precisamos dos valores que pode assumir e suas probabilidades.
Ou seja, vamos montar uma tabelinha, bem parecido como fazíamos nas questões de função de densidade!
Passo 3
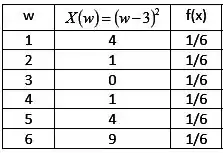
A ideia aqui é começar preenchendo todos os valores que pode assumir, e, depois disso, também podemos calcular os valores que pode assumir por meio da função dada no enunciado.
Sabemos que a probabilidade de sair cada número de um dado é . Dessa forma, preenchemos a coluna de . Com isso, descobrimos as probabilidades de cada valor que pode assumir!
Passo 4
Pô, agora que já temos todos os valores de probabilidade, podemos fazer nossa FDA!
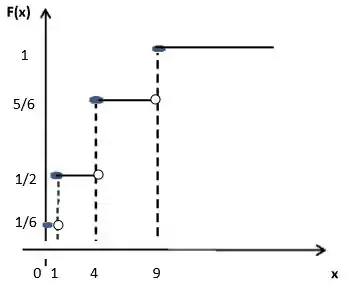
Tenha certeza que você lembra que a FDA de uma v.a. discreta é dado por um gráfico em forma de escada, e pra gente esboçar esse gráfico, basta calcularmos nossos “pulos”.
Começamos nosso gráfico com , onde temos . Como antes de não temos nenhuma probabilidade acumulada, essa probabilidade já é nosso primeiro “pulo”!
Passo 5
A ideia agora é procurar o próximo pulo, e isso ocorre no próximo valor que pode assumir, ou seja, .
Sabemos que:
Substituindo os valores, ficamos com:
Passo 6
Mantendo o mesmo raciocínio, vamos calcular o pulo em .
Passo 7
Agora, pra terminar, basta calcular para :
E chegamos no valor máximo da nossa FDA, que é 1!
Agora basta esboçar o gráfico e partir pro abraço.
Passo 8
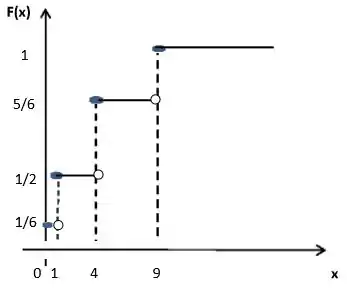
Resposta