Exercícios Resolvidos de Função de Probabilidade & Função de Distribuição Acumulada
Ver TeoriaEnunciado
Considere uma variável discreta com a seguinte função de probabilidade.
- Ache a constante que faz uma função de probabilidade.
- Encontre a função de distribuição ou função de distribuição acumulada? Plotar em gráfico esta função acumulada.
Passo 1
(a)
O que que uma função precisa pra ser considerada uma função de probabilidade? Isso você tem que saber, fundamental... a principal características dessas funções é que a integral ou o somatório delas tem que ser .
Nesse caso, como é uma função discreta (para valores fixos), não faz sentido integrar, então vamos fazer um somatório do valor dessa função, substituindo. E vamos igualar a , assim a gente descobre
Passo 2
Primeiro vamos substituir os valores de na função.
Somando agora todas essas parcelas, a gente tem que o somatório total é:
Passo 3
Agora é só igualar isso a pra descobrir o valor de .
Passo 4
(b)
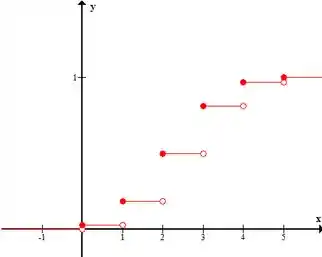
Como essa função é discreta, a gente sabe que nosso gráfico da acumulada vai ser aquela escadinha, concorda? Começando do zero e indo até o .
A cada valor de possível ( vamos dar um pequeno salto que representa o valor da probabilidade desse valor . A gente já conhece a probabilidade de cada valor possível de , é só substituir na função de probabilidade que a gente acabou de achar.
Por exemplo...
Passo 5
A nossa função acumulada , vai ser assim..
Nota que no final deu como já era de se esperar.
Passo 6
Agora é só montar o gráfico, vai ficar mais ou menos assim....
