Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Função de Probabilidade & Função de Distribuição Acumulada

Ver Teoria
Exercício 213456789101112131415161718192021

Enunciado

Sabe-se que a v.a. X assume os valores 1, 2 e 3 e que sua f.d.a. F(x) é tal que>

F 1 - F 1 - = 1 3

F 2 - F 2 - = 1 6

F 3 - F 3 - = 1 2

Obtenha a distribuição de X, a f.d.a. F(x) e o gráfico.

Passo 1

Sabemos que

P ( X = x i ) é igual ao salto que a função F ( x ) dá no ponto x i

E que P X = x i = F x i - F x i - .

Então pelo enunciado sabemos que:

P X = 1 = 1 3 P X = 2 = 1 6

P X = 3 = 1 2

Montando sua tabela de distribuição teremos:

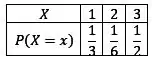
Passo 2

Agora vamos montar a f.d.a de X?

Temos quatro intervalos correto? Eles são

x < 1

1 ≤ x < 2

2 ≤ x < 3

x > 3

Para calcularmos a f.d.a de cada intervalo desse precisamos:

1º) Lembrar dos dados o enunciado

2º) Lembrar que estamos falando da distribuição acumulada portanto sempre precisamos olhar o intervalo anterior.

Vamos lá?

  • x < 1 → Bom, temos apenas três pontos no nosso enunciado e o primeiro é ponto 1 portanto antes dele podemos falar que F(X)=0.
  • 1 ≤ x ≤ 2 → Lembra da primeira coisa que falamos na questão? Aquele “F(X)-F((X-)” é o salto que a função dá naquele ponto. Sabemos que o “salto” que a função dá no ponto portanto nesse intervalo saltamos do 0 para do 1 3 .
  • 2 ≤ x ≤ 3 → Fazendo a mesm coisa que fizemos no item anterior podemos ver que nesse intervalo saltamos 1 6 . O erro aqui é pensar que por saltar isso estaremos nesse ponto. Lembre-se queremos a FUNÇÃO ACUMULADA. Nós estávamos no ponto 1 3 e saltamos 1 6 .   Assim chegaremos no ponto: 1 3 + 1 6 = 1 2 .
  • x > 3 → Agora já pegamos o jeito nisso né? Como salto foi de 1 2 e estávamos no ponto 1 2 , chegaremos no ponto: 1 2 + 1 2 = 1 .

Escrevendo mais bonitinho...

F X = 0 ,       x < 1 1 3 ,       1 ≤ x < 2 1 2 ,       2 ≤ x < 3 1 ,       x ≥ 3

Passo 3

Montando um gráfico:

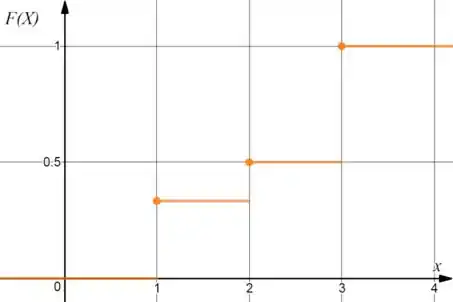
Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Na Tabela 2.4 tem-se a distribuição de freqüências dos salários de 36 funcionários, agrupados em classes de amplitude 4. Na Figura 2.7 tem-se o respectivo histograma. Reagrupando-se os dados em classe
Um sistema de controle de vôo de naves espaciais, chamado de PASS (Primary Avionies Software Set), usa quatro computadores independentes trabalhando em paralelo. Em cada etapa crítica, os computadores
Intervalos de classes desiguais. É muito comum o uso de classes com tamanhos desiguais no agrupamento dos dados em tabelas de freqüências. Nestes casos deve-se tomar alguns cuidados especiais quanto à
Um arranjo consiste em três componentes mecânicos. Suponha que as probabilidades do primeiro, do segundo e do terceiro componentes satisfazerem as especificações sejam iguais a 0.95, 0.98 e 0.99. Cons
Duas cartas são escolhidas aleatoriamente de um baralho de 52 cartas. Qual é a probabilidade de(a) ambas serem ases?(b) ambas terem o mesmo valor?