Exercícios Resolvidos de Função de Probabilidade & Função de Distribuição Acumulada
Ver TeoriaEnunciado
Probabilidade e Estatística – PUC RJ – 2019.2 – P1 – Questão 1
Uma variável aleatória discreta tem a seguinte função de probabilidade:
Pede-se:
Calcular o valor do parâmetro , detalhando os passos para que seja uma função de probabilidade. Apresente a função de probabilidade e seu domínio.
Passo 1
Fala pessoal, bora resolver mais uma questão de PROBEST?
Nessa questão vamos trabalhar com uma distribuição de probabilidade discreta com . Isso significa que deve ser um inteiro positivo, caso não seja, a probabilidade é nula, o que é descrito pela última linha da função dada no enunciado.
Se ou , temos que . Já para inteiro, temos . A primeira coisa que devemos fazer é determinar o valor da constante para que a função de probabilidade seja normalizada. Isso significa que a soma de todas as probabilidades deve ser igual a :
Repare que eu escrevi sem fim, já que existem infinitos valores de inteiros positivos.
Passo 2
Para e temos:
Já para :
E assim por diante...
O próximo passo é substituir tudo na condição de normalização:
Ou ainda,
Passo 3
Repare que o termo infinito é a soma de uma PG onde o primeiro termo é
e a razão é
Com isso, o segundo termo é
E assim por diante...
Como a razão dessa PG é , a soma dessa PG infinita converge para
Portanto,
Desta forma, a condição de normalização fica
Agora podemos achar :
Passo 4
Com isso, a função de probabilidade pode ser escrita como
A seguir faço um esboço da função:
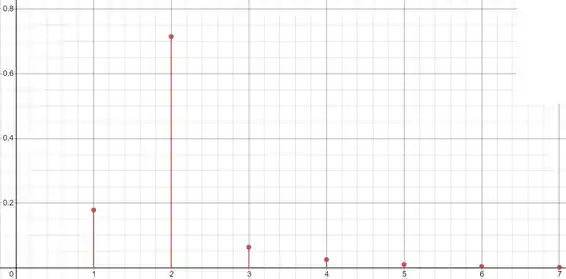
Note que para a probabilidade vai ficando cada vez menor. OBS: a distribuição não acaba em , ela continua para , mas seus valores ficam cada vez menores.