Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Função de Probabilidade & Função de Distribuição Acumulada

Ver Teoria
Exercício 131234567891011121415161718192021

Enunciado

Prova P1 – 2019.1– USP – Probabilidades – Teste 6

Uma cozinheira prepara bolos e deixa a massa descansar um tempo aleatório entre 1 e 3 minutos após o que os coloca no forno. Um estagiário verificou que os bolinhos que descansavam mais de 2 minutos ficavam mais duros que o normal. A densidade de probabilidades do tempo de descanso é f ( t )   =   k t 2 . A probabilidade de dois bolinhos em três produzidos ficarem muito duros é:

  1. n . d . a . ;
  2. 19 26 2 ;
  3. 3 19 26 2 7 26 ;
  4. 3 7 26 10 26   ;
  5. 7 26 19 26 .

Passo 1

Faaalaeee menó, beleza?

Seguinte, a gente sabe que a função densidade de probabilidade (FDP) é dada da seguinte forma para variáveis contínuas:

∫ - ∞ ∞ f x = 1

Em que temos dois intervalos de tempo de descanso dos bolinhos:

  • De 1 a 2 segundos;
  • De 2 a 3 segundos.

Ou seja, sabemos que a probabilidade durante esses 3 minutos é de 100 %. Logo:

P 1 ≤ t < 2 + P 2 ≤ t ≤ 3 = 1

Passo 2

Assim, pela FDP dada na questão, temos:

∫ 1 2 k t 2 d t + ∫ 2 3 k t 2 d t = 1 ∴

k t 3 3 2 1 + k t 3 3 3 2 = 1 ∴

7 k 3 + 19 k 3 = 1 ∴

k = 3 26

Passo 3

Dessa forma, para que dois bolinhos de três estejam duros, temos:

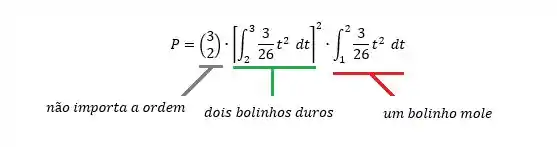
Resolvendo a equação, temos:

P = 3 3 26 t 3 3 3 2 2 ∙ 3 26 t 3 3 2 1 ∴

P = 3 3 26 19 3 2 ∙ 3 26 t 3 3 2 1 ∴

P = 3 19 26 2 7 26

Entendeu direitinho??? Valeeeu!

Resposta

P = 3 19 26 2 7 26

Exercícios de Livros Relacionados

Na Tabela 2.4 tem-se a distribuição de freqüências dos salários de 36 funcionários, agrupados em classes de amplitude 4. Na Figura 2.7 tem-se o respectivo histograma. Reagrupando-se os dados em classe
Um sistema de controle de vôo de naves espaciais, chamado de PASS (Primary Avionies Software Set), usa quatro computadores independentes trabalhando em paralelo. Em cada etapa crítica, os computadores
Intervalos de classes desiguais. É muito comum o uso de classes com tamanhos desiguais no agrupamento dos dados em tabelas de freqüências. Nestes casos deve-se tomar alguns cuidados especiais quanto à
Um arranjo consiste em três componentes mecânicos. Suponha que as probabilidades do primeiro, do segundo e do terceiro componentes satisfazerem as especificações sejam iguais a 0.95, 0.98 e 0.99. Cons
Duas cartas são escolhidas aleatoriamente de um baralho de 52 cartas. Qual é a probabilidade de(a) ambas serem ases?(b) ambas terem o mesmo valor?