Três bolas enumeradas e estão num balde. Sorteamos duas bolas, e somamos os valores obtidos. Seja este valor.
- Obter a função de probabilidade de se as bolas forem sorteadas com e sem reposição.
- Em ambos os casos, desenhar a função de distribuição acumulada de .
Passo 1
Vamos começar com o caso com reposição!
é o valor da soma das duas bolas sorteadas, beleza? Temos primeiro que montar a função de probabilidade de .
Quais são os possíveis valores de ? Se é a soma de duas bolas retiradas com reposição e as bolas são e , então os possíveis valores são:
Note que , a ordem importa. Então a gente tem combinações de resultados pra retirada das duas bolas.
Desse jeito a gente tem que os possíveis valores de são: .
Nossa variável é uma v.a. discreta, concorda? Seus possíveis valores são números fixos, não tem como a soma das duas bolas resultar em !
Passo 2
Pra montar a função de probabilidade de uma v.a. discreta, a gente precisa montar aquela tabelinha, com os possíveis valores de e a probabilidade de cada um desses valores acontecer.
Os possíveis valores a gente já tem: .
Agora falta calcular a probabilidade de cada um, que é tranquilo.
Vamos começar por .
A soma das duas bolas só resulta em em uma das combinações de bolas, quando sai , daí:
Pensando dessa mesma forma a gente consegue todas as prob. que a gente quer.
Você pode até conferir se tá tudo certin, é só ver se a soma de todas as probabilidades dá .
Você pode deixar sua resposta final assim, ou se tiver com tempo sobrando, colocar arrumado numa tabela maneira.
Passo 3
Po, agora vai ser sem reposição, o que que muda? Muda que resultados como e não vão ser possíveis, certo?
Então os únicos resultados possíveis são:
E assim, os possíveis resultados pra nossa v.a. soma das duas bolas, vai ser:
Passo 4
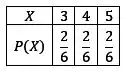
Agora é o mesmo esquema pra calcular a probabilidade de cada resultado possível de .
É isso aí, dá pra você organizar numa tabela se preferir.
Passo 5
Função de distribuição acumulada é aquela que parece uma escada, que sempre que você chega num possível valor de você sobe (acumula) o valor da probabilidade desse valor de .
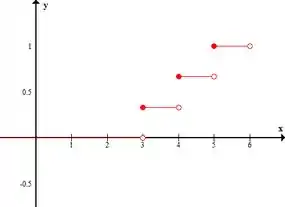
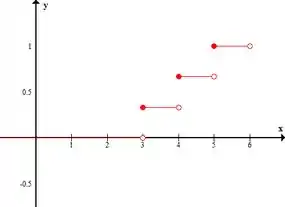
Pra primeira situação, com reposição, ficaria:
Ali quando , sobe para , depois em
E por aí em diante, acumulando os valores, até chegar em .
Passo 6
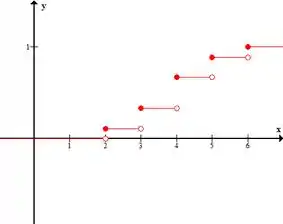
Para o caso sem reposição, o gráfico fica assim:
Subindo em cada valor de .
Resposta
Com reposição:
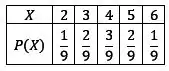
Sem reposição:
Com reposição:
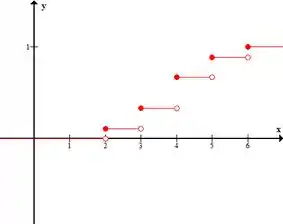
Sem reposição: