Exercícios Resolvidos de Função de Probabilidade & Função de Distribuição Acumulada
Ver TeoriaEnunciado
Uma urna contém três bolas numeradas de 1 a 3. Suponha que vamos fazer um sorteio sem reposição de duas bolas dessa urna. Considere uma variável aleatória discreta que represente a diferença em módulo dos valores entre as bolas. Monte a função de probabilidade dessa variável e o gráfico da FDA.
Passo 1
Sabemos que:
Fazemos um sorteio sem reposição, então podemos tirar as seguintes combinações de bolas:
Certo? E a diferença para cada um desses casos é:
Então nossa variável pode assumir os valores 1 e 2. E quais são as probabilidades de cada um desses valores ocorrem?
Então nossa função de probabilidade fica:
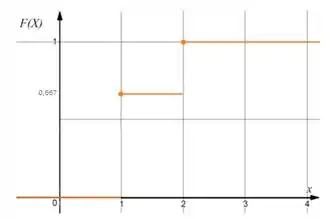
E o gráfico da FDA vai ficar:
Passo 2
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Na Tabela 2.4 tem-se a distribuição de freqüências dos salários de 36 funcionários, agrupados em classes de amplitude 4. Na Figura 2.7 tem-se o respectivo histograma. Reagrupando-se os dados em classe
Um sistema de controle de vôo de naves espaciais, chamado de PASS (Primary Avionies Software Set), usa quatro computadores independentes trabalhando em paralelo. Em cada etapa crítica, os computadores
Intervalos de classes desiguais. É muito comum o uso de classes com tamanhos desiguais no agrupamento dos dados em tabelas de freqüências. Nestes casos deve-se tomar alguns cuidados especiais quanto à
Um arranjo consiste em três componentes mecânicos. Suponha que as probabilidades do primeiro, do segundo e do terceiro componentes satisfazerem as especificações sejam iguais a 0.95, 0.98 e 0.99. Cons
Duas cartas são escolhidas aleatoriamente de um baralho de 52 cartas. Qual é a probabilidade de(a) ambas serem ases?(b) ambas terem o mesmo valor?