Listas de Estudos UFES - Cálculo 1 de Cálculo 1 da UFES - Lista 9

Determine a expressão de pelo menos duas funções definidas implicitamente pela equação . Explicite seus domínios.

Um ponto move-se ao longo da elipse . A abcissa está variando a uma velocidade . Mostre que

Um ponto move-se sobre a semicircunferência . Suponha . Determine o ponto da curva em que a velocidade de seja o dobro da velocidade de .

Uma escada de está encostada numa parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?

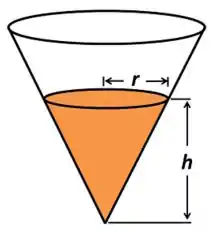
Enche-se de água um reservatório, cuja forma é de um cone circular reto (veja a figura), a uma taxa de . O vértice está a do topo e o raio do topo é de . Com que velocidade o nível da água está subindo no instante em que ?

O raio de luz de um farol, que está situado a de uma praia reta, faz (rotações por minuto). Considere a altura do farol desprezível em relação a sua distância até à praia. Ache a velocidade da extremidade do raio de luz, no longo da praia, quando ele faz um ângulo de com a linha da praia.

Seja definida implicitamente pela equação . Calcule , sabendo que .

Seja definida implicitamente pela equação . Encontre o coeficiente angular da reta normal ao gráfico da função no ponto .

Considere definida implicitamente por . Calcule , sabendo que , .

Considere a curva da figura ao lado conhecida como cissóide de Diócles cuja equação é .

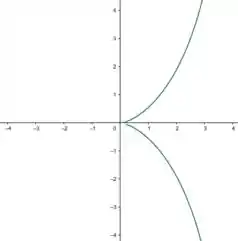
1. Obtenha a equação da reta tangente ao gráfico da curva em ;

Considere a curva da figura ao lado conhecida como cissóide de Diócles cuja equação é .

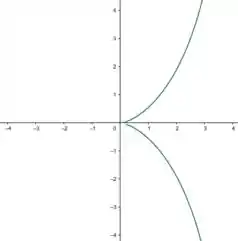
b) Obtenha as equações das retas tangentes ao gráfico da curva nos pontos em que .

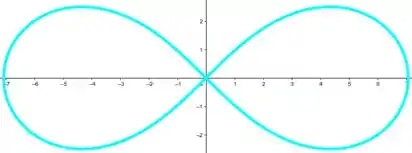
Considere a leminiscata de equação (figura ao lado). Determine os quatro pontos da leminiscata em que as retas tangentes são horizontais. Ache, em seguida, os dois pontos em que as tangentes são verticais.

Uma câmara de televisão no nível do solo está filmando a subida de um ônibus espacial que está subindo verticalmente de acordo com a equação , sendo a altura e o tempo. A câmara está a do local de lançamento. Encontre a taxa de variação da distância entre a câmara e a base do ônibus espacial, após o lançamento (suponha que a câmara e a base do ônibus estão no mesmo nível no tempo).

Num determinado instante, um controlador de tráfego aéreo vê dois aviões na mesma altura voando a velocidades constantes, em trajetórias ortogonais que se cruzam num ponto (veja figura). Neste instante, um dos aviões está a milhas do ponto e se aproxima de à milhas por hora, enquanto o outro está a milhas do ponto e se movendo à milhas por hora, também em direção ao ponto .

1. Antes do ponto , a distância entre os aviões está diminuindo? A que taxa?

Num determinado instante, um controlador de tráfego aéreo vê dois aviões na mesma altura voando a velocidades constantes, em trajetórias ortogonais que se cruzam num ponto (veja figura). Neste instante, um dos aviões está a milhas do ponto e se aproxima de à milhas por hora, enquanto o outro está a milhas do ponto e se movendo à milhas por hora, também em direção ao ponto .

b) Os aviões correm risco de choque? Em caso afirmativo, quanto tempo o controlador tem

para fazer com que um dos aviões mude a sua trajetória?