Exercícios Resolvidos de Reta Tangente – Derivadas Implícitas

Exercício 30 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

Enunciado

Lista 9 – 2018.1 – UFES – Cálculo 1 – Questão 6

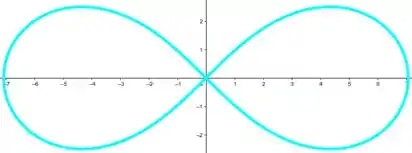
Considere a leminiscata de equação (figura ao lado). Determine os quatro pontos da leminiscata em que as retas tangentes são horizontais. Ache, em seguida, os dois pontos em que as tangentes são verticais.

Passo 1

Falaeee, beleza?? Seguinte... primeiramente derivaremos implicitamente:

Passo 2

Nos pontos em que a tangente é horizontal, . Assim, temos:

Dessa expressão, desconsiderando o resultado e , temos:

Passo 3

Substituindo esses valores de na função original, temos que:

E, para cada valor de , temos que é:

Para : ;
Para : .

Dessa forma, temos os pontos cuja reta tangente é a horizontal:

Passo 4

Já para que a tangente seja vertical, vemos, pelo gráfico, que obrigatoriamente deve ser igual a . Assim, temos que:

Desconsiderando , temos:

Portanto, os pontos em que a tangente é vertical, são:

Entendeu direitinho?? Responde Aí haha

Resposta

Pontos da horizontal:

Pontos na vertical:

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado. y 2 y 2 - 4 = x 2 ( x 2 - 5 ) , ( 0 , - 2 ) (curva do diabo)

Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado. x 2 + y 2 = 2 x 2 + 2 y 2 - x 2 , 0 , 1 2 (cardioide)

Encontre as equações de ambas as retas tangentes para a elipse x 2 + 4 y 2 = 36 que passem pelo ponto ( 12 ,3 ) .

Duas curvas são ortogonais se suas retas tangentes forem perpendiculares em cada ponto de interseção. Mostre que as famílias dadas de curvas são trajetórias ortogonais uma em relação à outra, ou seja,

28. Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado. x 2 + 2 x y - 4 y ² = 12 ² , ( 2,1 ) (elipse)