Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 381234567891011121314151617181920212223242526272829303132333435363739404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Lista 9 – 2018.1 – UFES – Cálculo 1 – Questão 8

Uma câmara de televisão no nível do solo está filmando a subida de um ônibus espacial que está subindo verticalmente de acordo com a equação s = 15 t 2 , sendo s a altura e t o tempo. A câmara está a 600   m do local de lançamento. Encontre a taxa de variação da distância entre a câmara e a base do ônibus espacial, 10   s e g após o lançamento (suponha que a câmara e a base do ônibus estão no mesmo nível no tempo t = 0 ).

Passo 1

Falaeee, beleza?? Seguinte... observando a imagem abaixo, podemos dizer que a distância d é dada da seguinte forma:

d 2 = s 2 + 600 2

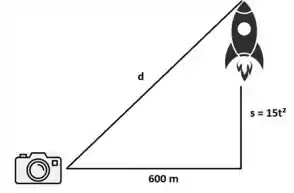
Passo 2

Derivando a expressão implicitamente em relação ao tempo e isolando a taxa de variação da distância, temos:

2 d d ' = 2 s s ' + 0 ∴

d ' = s s ' d

Passo 3

Além disso, para t = 10   s e g , temos que:

s = 15 t 2 ∴ s = 15 ∙ 10 2 ∴ s = 1500 m

E que sua derivada é dada por:

s ' = d d t 15 t 2 ∴ s ' = 30 t ∴ s ' = 30 ∙ 10 ∴ s ' = 300

Além disso, substituindo na primeira fórmula que fizemos no passo 1, temos:

d 2 = 1500 2 + 600 2 ∴ d = 1615,55   m

Passo 4

Assim, substituindo esses valores na equação mostrada no passo 2, temos:

d ' = 1500 ∙ 300 1615,55 ∴

d ' = 278,54   m

Entendeu direitinho?? Responde Aí haha

Resposta

d ' = 278,54   m

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s