Lista 9 – 2018.1 – UFES – Cálculo 1 – Questão 13
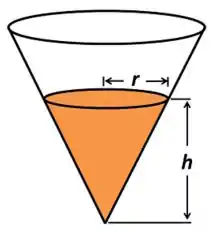
Enche-se de água um reservatório, cuja forma é de um cone circular reto (veja a figura), a uma taxa de . O vértice está a do topo e o raio do topo é de . Com que velocidade o nível da água está subindo no instante em que ?
Passo 1
Falaeee, beleza?? Seguinte... Nós temos que o volume de um cone é dado por:
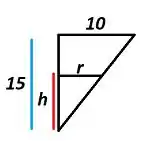
E, fazendo uma semelhança de triângulos, vemos também que:
Passo 2
Portanto, temos que, para :
Derivando essa função explicitamente quanto ao tempo, temos:
Passo 3
Assim, sendo e , temos para :
Entendeu direitinho?? Responde Aí haha
Resposta
Exercícios de Livros Relacionados
20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s