Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 361234567891011121314151617181920212223242526272829303132333435373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Lista 9 – 2018.1 – UFES – Cálculo 1 – Questão 9a

Num determinado instante, um controlador de tráfego aéreo vê dois aviões na mesma altura voando a velocidades constantes, em trajetórias ortogonais que se cruzam num ponto P (veja figura). Neste instante, um dos aviões está a 150 milhas do ponto P e se aproxima de P à 450 milhas por hora, enquanto o outro está a 200 milhas do ponto P e se movendo à 600 milhas por hora, também em direção ao ponto P .

  1. Antes do ponto P , a distância entre os aviões está diminuindo? A que taxa?

Passo 1

Eaeee, beleza? Olha, vamos ver a seguinte figura para deixar melhor o nosso entendimento:

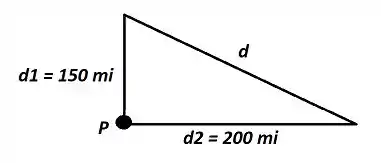
Inicialmente, podemos deduzir que:

d = 150 2 + 200 2 ∴ d = 250   m i

Passo 2

Sendo d 2 = d 1 2 + d 2 2 , derivando a expressão implicitamente, temos:

2 d d ' = 2 d 1 d 1 ' + 2 d 2 d 2 '

Lembrando que, inicialmente:

  • d 1 ' = 450   m i / h
  • d 2 ' = 600   m i / h

Passo 3

Dessa forma, substituindo as taxas de variação e as distâncias iniciais, temos para d ' :

2 ∙ 250 d ' = 2 ∙ 150 ∙ 450 + 2 ∙ 200 ∙ 600 ∴

d ' = 750   m i / h

s = 15 t 2 ∴ s = 15 ∙ 10 2 ∴ s = = 1500 m

E que sua derivada é dada por:

s ' = d d t 15 t 2 ∴ s ' = 30 t ∴ s ' = 30 ∙ 1 0

∴ s ' = 300

Além disso, substituindo na primeira fórmula que fizemos no passo 1, temos:

d 2 = 1500 2 + 600 2

∴ d = 1615,55   m

Entendeu direitinho?? Responde Aí haha

Resposta

d = 1615,55   m

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s