Considere a curva da figura ao lado conhecida como cissóide de Diócles cuja equação é .
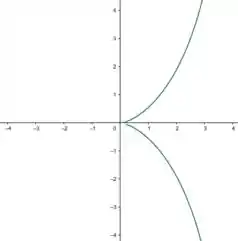
- Obtenha a equação da reta tangente ao gráfico da curva em ;
Passo 1
Falaeee, beleza?? Seguinte, primeiramente vamos derivar a função implicitamente para determinar o coeficiente angular da tangente da curva no ponto :
Passo 2
Assim, substituindo , temos:
Passo 3
Com o coeficiente angular igual a e passando pelo ponto , é possível determinarmos a reta:
Logo, temos a reta
Entendeu direitinho?? Responde Aí haha
