Lista 9 – 2018.1 – UFES – Cálculo 1 – Questão 14
O raio de luz de um farol, que está situado a de uma praia reta, faz (rotações por minuto). Considere a altura do farol desprezível em relação a sua distância até à praia. Ache a velocidade da extremidade do raio de luz, no longo da praia, quando ele faz um ângulo de com a linha da praia.
Passo 1
Falaeee, beleza?? Seguinte... Vamos primeiro fazer uma pequena representação da questão para ficar melhor de a gente entender hehe
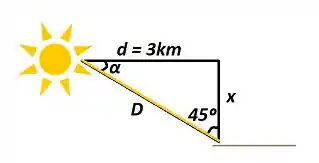
Da figura, temos que:
E que:
Passo 2
Agora, derivamos explicitamente ambas as expressões. Da primeira, temos:
E, da segunda expressão, temos:
Passo 3
Como queremos a velocidade do feixe de luz na praia, devemos determinar . Para isso, temos as grandezas a seguir:
- (pois trata-se de um triângulo isósceles);
- ;
- (complementar de );
- ou ;
Ainda, da primeira equação do passo 2, temos que:
Passo 4
Dessa forma, substituindo os valores na segunda equação do passo 2, temos:
Entendeu direitinho?? Responde Aí haha
