Considere a curva da figura ao lado conhecida como cissóide de Diócles cuja equação é .
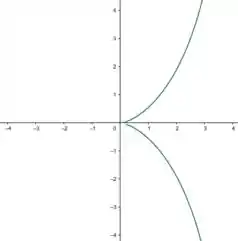
b) Obtenha as equações das retas tangentes ao gráfico da curva nos pontos em que .
Passo 1
Falaeee, beleza?? Seguinte... quando , temos os seguintes valores para :
Passo 2
Para esses dois valores de , podemos determinar os coeficientes angulares:
Para
Para é o mesmo cálculo, mas com o sinal invertido. Assim, temos que:
Passo 3
Com os coeficientes e pontos, podemos encontrar as retas:
Para e :
Logo,
E, para e :
Assim,
Entendeu direitinho?? Responde Aí haha
