P1 de Cálculo 1 da UFRJ - 2020.2

. Considere a função . Então satisfaz a equação

A derivada da função é dada por

Seja uma função inversível e diferenciável tal que e . Então a equação da reta tangente ao gráfico da função inversa em é:

Seja , onde e é função derivável em . Sabendo que e podemos concluir que é igual a

. Considere o ponto deslocando-se sobre o gráfico

, para ,

Onde e são medidos em centímetros. Denotemos por o ponto dado pela interseção do eixo com a reta tangente ao gráfico de no ponto . Sabendo que a coordenada do ponto varia a uma taxa constante de , determine com que taxa estará variando a coordenada do ponto no instante em que as coordenadas do ponto forem .

A equação

tem exatamente uma raiz real positiva, mas não tem uma raiz real negativa.

tem pelo menos três raízes reais.

: não tem raízes reais.

tem exatamente duas raízes reais.

tem exatamente uma raiz real negativa, mas não tem uma raiz real positiva.

Considere as afirmações a seguir

Seja uma função diferencial em tal que e . Então existe tal que ;

Seja uma função diferencial em e suponha que existe tal que . Então ;

Sejam e funções diferenciáveis em tais que para todo e suponha, além disso, que . Então .

Podemos concluir com certeza que:

: Apenas a afirmação é verdadeira.

: Apenas as afirmações e são verdadeiras.

: Todas as afirmações são verdadeiras.

: Apenas as afirmações e são verdadeiras.

: Apenas as afirmações e são verdadeiras.

Na figura abaixo, o segmento mede e é tangente à circunferência de raio no ponto . O ponto é determinado pela interseção da circunferência com o segmento . O ponto inicia um movimento de descida, pela vertical, em direção ao ponto a uma taxa constante de .

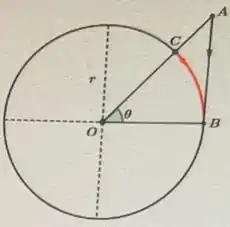
A taxa com que se movimenta o ponto , ao longo do arco , depois de segundos do ponto ter iniciado o seu movimento é

:

:

:

:

:

Seja . Considere as seguintes afirmações:

A função não tem um mínimo nem um máximo local em .

A curva tem um ponto de inflexão em

não existe.

A função é crescente em .

Sobre as afirmações acima, podemos concluir que

e são verdadeiras e e são falsas.

e são verdadeiras e é falsa.

e são verdadeiras e é falsa.

e são verdadeiras e é falsa.

As quatro afirmações são verdadeiras.

Dada a função , considere as afirmações:

não é ponto de mínimo local nem ponto de máximo local de .

é ponto de máximo local de .

é ponto de mínimo local de .

não possui nem mínimo nem máximo locais.

Selecione a opção correta:

As quatro afirmações são falsas.

A afirmação é verdadeira e as demais são falsas.

As afirmações e são verdadeiras e as demais são falsas.

A afirmação é verdadeira e as demais são falsas.

A afirmação é verdadeira e as demais são falsas.

Seja uma função tal que . Então podemos afirmar que:

para todo .

.

Existe tal que .

para todo .

.

Questão 4 - A superfície de um cubo oco, de aresta , é feita de um material que se encolhe uniformemente a uma taxa constante de . Determine com que taxa está diminuindo o volume do cubo no momento em que sua aresta mede .

Questão 4 - A superfície de um cubo oco, de aresta , é feita de um material que se encolhe uniformemente a uma taxa constante de . Determine com que taxa está diminuindo o volume do cubo no momento em que sua aresta mede .

Questão 4 - A superfície de um cubo oco, de aresta , é feita de um material que se encolhe uniformemente a uma taxa constante de . Determine com que taxa está diminuindo o volume do cubo no momento em que sua aresta mede .

Calcule os seguintes limites:

Questão 4 - A superfície de um cubo oco, de aresta , é feita de um material que se encolhe uniformemente a uma taxa constante de . Determine com que taxa está diminuindo o volume do cubo no momento em que sua aresta mede .