UTFPR – Cálculo 2 – P1 2021.1 – Questão 1
Determine e faça o esboço do domínio da função
Passo 1
Oiii pessoal, tudo bem?
Se liga, nesse exercício temos essa função
E aí queremos encontrar o domínio dela
Só pra lembrar, em uma função de várias variáveis, o domínio vai incluir todos os pontos , exceto os que
- Fazem a raíz ser negativa
- Fazem o denominador zerar
- Fazem o logaritmando ser menor ou igual a 0
Então vamos ver quais são os valores de e/ou que fazem alguma dessas coisas acontecer, porque aí eles vão estar fora do domínio
Passo 2
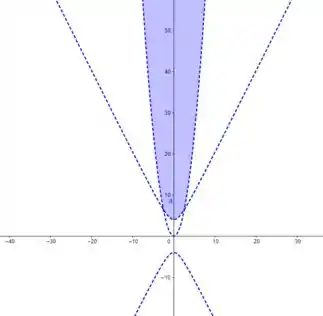
Pra começar, temos um logaritmo no numerador da função. O logaritmando precisa ser sempre maior do que , então:
Então temos a região acima da parábola
Passo 3
Além disso, temos uma raíz quadrada no denominador. Isso vai ter que ser pra termos uma raíz positiva (não pode ser igual a zero pra não zerar o denominador). Então olha:
Dividindo tudo por :
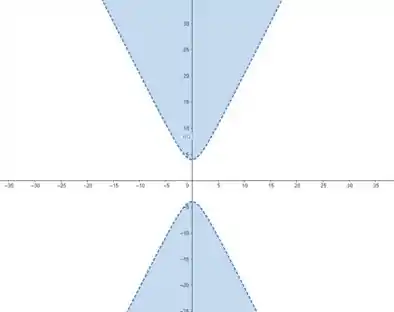
Isso forma a equação de uma hipérbole ao longo do eixo (porque é o quem está negativo) com e .
A distância entre os vértices é e a hipérbole é centrada na origem, assim:
Passo 4
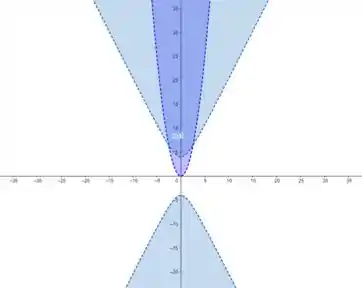
Então, o nosso domínio vai incluir todos os pontos , exceto os que deram problema nos itens anteriores:
E a região que cumpre essas duas condições é a região formada pela intersecção entre os gráficos dos itens anteriores:
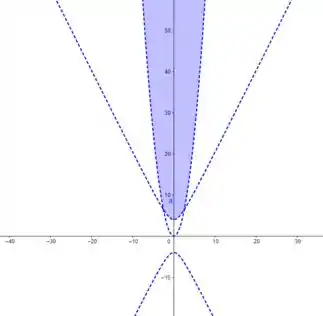
Sucesso entãooo
Resposta
