Seja uma função tal que . Então podemos afirmar que:
para todo .
.
Existe tal que .
para todo .
.
Passo 1
Vem comigo que a gente detona com essa questão juntos!
A função que o enunciado nos deu, não é uma função que que se integral com facilidade e teríamos que usar métodos que fogem da matéria de cálculo .
Para avaliar podemos esboçar o gráfico dela de forma simplificada a partir do gráfico de , tendo esse gráfico simplificado de podemos ver qual alternativa é a correta.
O gráfico de é da seguinte forma:
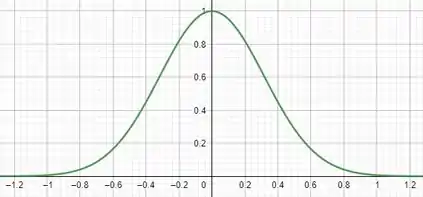
Passo 2
Vamos avaliar o gráfico de .
A gente ver no gráfico que ele tende a zero pra e para , isso quer fizer que o gráfico de nesse limites tendem a um valor constante já que a derivada de uma constante é zero.
Só que para tende a uma constante positiva e para tende a uma constante negativa , isso vem por conta da simetria do gráfico de .
No ponto temos o máximo de e quando a derivada tem um máximo ou um mínimo em um certo ponto a função é igual a zero nesse ponto, então .
Como já vimos mais acima a função vem de uma tendência ao valor negativo conforme cresce e depois vai para uma tendencia ao valor positivo e o único ponto onde ela encosta no eixo é em , então esse ponto é um ponto de inflexão.
Com essas análises podemos ter o seguinte esboço do gráfico de .
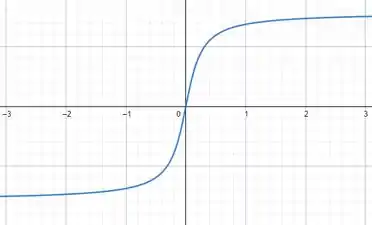
Passo 3
As alternativas do enunciado estão relacionadas ao deslocamento do gráfico, da seguinte maneira, quando temos fazemos a seguinte operação nós fazemos o gráfico andar para direita ou para a esquerda .
Quando fazemos a operação nós fazemos o gráfico andar para cima ou para baixo .
Então é com base nisso que vamos encontrar a alternativa correta.
Passo 4
Vamos começar com o item .
Temos o seguinte:
Quando fazemos deslocamos o gráfico para a esquerda então o máximo que a função pode atingir ainda é , agora quando fazemos nós pegamos esse valor máximo de e somamos , então , logo:
Quando fazemos a função andar para a esquerda a gente bem dizer faz valores de menores atingirem valores maiores em , então:
Então essa alternativa é a correta! Que sorte, finalizamos o trabalho logo com a primeira.
Resposta
para todo .