Considere as regiões e definidas a seguir.
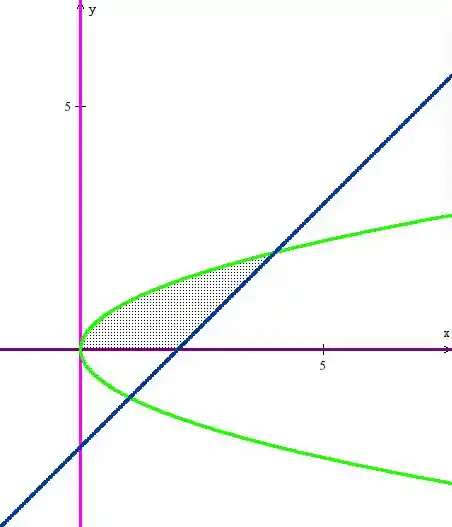
é a região do primeiro quadrante limitada pela curva , pelo eixo e pela reta .
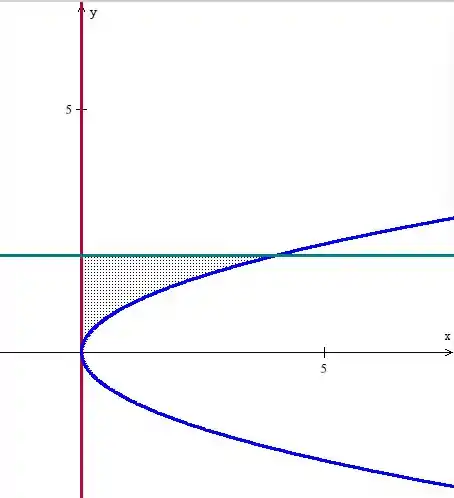
é a região limitada pela curva , pelo eixo e pela reta .
Sem calcular as integrais, faça o que se pede a continuação.
- Faça o esboço de e de .
- Escreva uma integral, ou uma soma de integrais, que expresse a área da região .
- Escreva uma integral, ou uma soma de integrais, que expresse o volume do sólido obtido pela rotação de em torno do eixo .
- Escreva uma integral, ou uma soma de integrais, que expresse o volume do sólido obtido pela rotação de em torno da reta .
Passo 1
Apesar de ter muita coisa para fazer nessa questão, não é necessário calcular as integrais, e isso já ajuda bastante.
Vamos começar pela letra e esboçar a as regiões.
está no primeiro quadrante, entre e e sob a curva , que é uma parábola virada. Temos também a reta entrando na história, ficando:
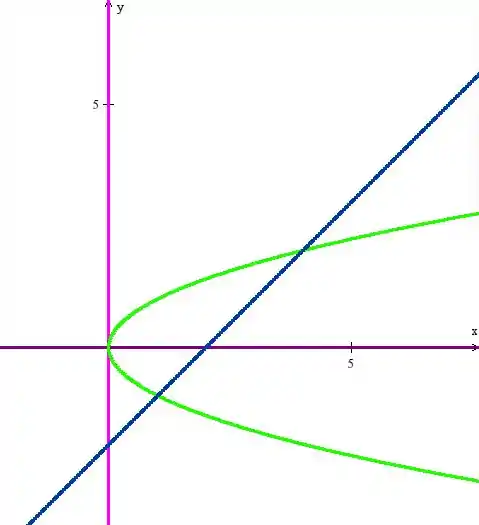
Agora, racharemos a interseção entre as curvas e essa será a região .
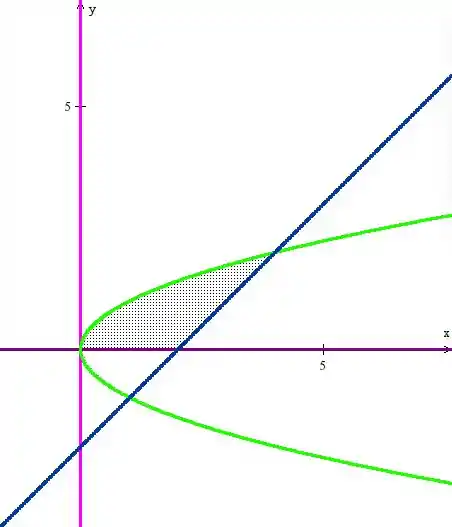
Passo 2
Agora, vamos para . é a região limitada pela curva , pelo eixo e pela reta .
Ou seja, temos a mesma parábola tombada, o eixo e a reta , ficando:
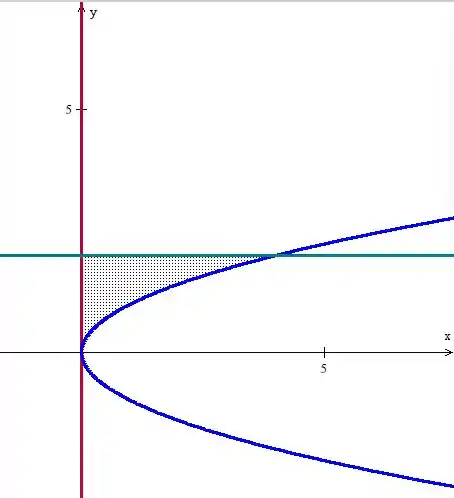
Pronto, esboçamos as regiões!
Passo 3
Vamos tentar expressar a área de por integrais agora. Observe o esboço da região e veja que a curva superior é sempre a parte de cima da parábola , ou seja:
Porém, a curva inferior muda. Uma hora é o eixo e outra passa a ser a reta . Dessa maneira, precisamos dividir a região em duas e calcular usando duas integrais.
Precisamos ainda determinar o intervalo de integração dessas integrais. Considerando a primeira como sendo aquela com curva inferior sendo o eixo , vemos, pelo gráfico que o limite inferior de integração é e o superior é justamente o ponto onde a curva inferior deixa de ser o eixo e passa a ser a reta , ou seja, na interseção desta reta com o eixo , em:
Opa! Temos o limite de integração e as curvas, podemos escrever a primeira integral:
Vamos para a segunda agora. A segunda começa exatamente onde a primeira termina, ou seja, o limite inferior de integração é . O limite superior será a na interseção da reta com a meta de superior da parábola, ou seja, em:
Elevando ao quadrado e isolando :
Como , ficamos com . Esse será o limite superior de integração. Temos a segunda integral agora:
A área da região será a soma das duas áreas:
Passo 4
Agora precisamos representar o volume de revolução de em torno do eixo por integrais. Como estamos girando em torno do eixo , podemos usar o método dos discos cilíndricos.
Observando o esboço da região novamente, dá para perceber que o volume é o volume da rotação da curva superior menor o volume de rotação da reta
Assim, teremos:
Agora, a reta não começa em , ela só toca o eixo em , como calculamos anteriormente. Assim:
Logo, o volume será:
Passo 5
- Escreva uma integral, ou uma soma de integrais, que expresse o volume do sólido obtido pela rotação de em torno da reta .
Ainda não acabou! Falta rotacionar a região em torno da reta . Novamente, podemos usar o método dos discos cilíndricos, mas temos que olhar com cuidado o esboço.
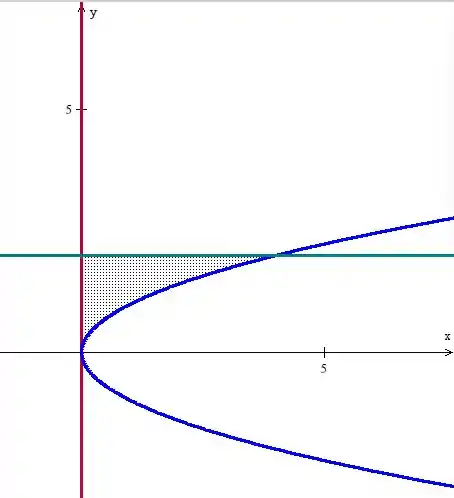
Rodar essa região em torno da reta , consiste simplesmente em roda parte de cima da parábola em torno de . O limite inferior de integração visivelmente é zero, o superior é a interseção de com a reta . Vamos calcular:
Assim:
Pronto, é isso!
Resposta