Seja a região do plano delimitada inferiormente pelo eixo , superiormente pelo gráfico de , à esquerda pela reta e à direita pela reta .
Se a area , entao
Passo 1
Primeiro, vamos traçar pensar no esboço dessa tal região .. Ela está limitada entre o eixo e uma função desconhecida :
Agora, traçamos a reta , uma reta qualquer e limitamos a região entre elas:
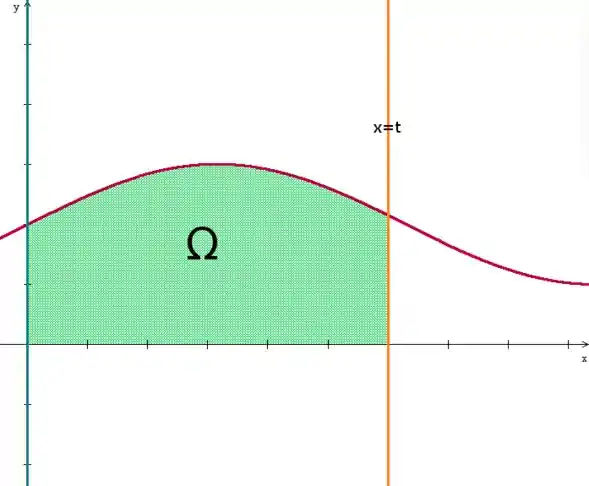
Passo 2
Agora que traçamos a região, vamos analisar como seria a integral que dá origem a sua área. Temos uma região entre as retas e . Esse será então o nosso intervalo de integração.
Temos a área limitada pela curva . Ou seja, a área da região será:
Passo 3
Hmmm... Sabemos o quanto dá a integral, mas não sabemos qual é o integrando . Precisamos chegar nele de alguma forma...
Como a derivação é a operação inversa da integração, se derivarmos a integral, conseguimos chegar ao integrando. Então vamos lá, derivando dos dois lados.
Pelo Teorema fundamental do Cálculo, temos que:
Pela regra do produto e cadeia:
Igualando essa felicidade:
Opah!

Chegamos na expressão de . Agora é só substituir no ponto desejado.
Passo 4
Letra a!