Considere a região destacada na figura abaixo que é delimitada pelas curvas e .
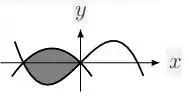
A área de é dada por:
Passo 1
Pela figura, já para saber que o limite superior de integração dessa curva é . Vamos fazer a interseção entre elas para achar o intervalo inferior de integração:
Excluindo da solução, podemos cortá-lo:
Resolvendo essa equação aí, encontramos:
é maior que zero, então vamos ficar com o . Esse será o limite inferior de integração.
Passo 2
Legal, agora precisamos saber que curva é maior no intervalo. Para tal, só pegar qualquer valor no intervalo e ver qual é maior. Pegando :
Como , a segunda curva será a curva superior e a primeira a inferior.
Passo 3
Sabendo de tudo, só montar a integral no formato:
O intervalo de integração será como já visto. O integrando será:
Ficando:
Que é exatamente a letra !
Resposta
Letra a.