Seja uma função qualquer derivável em todos os pontos de . Considere as afirmativas abaixo:
- Se , então com certeza não é um máximo local de .
- Se , então com certeza é um mínimo ou máximo local de .
É verdadeira ou são verdadeiras:
- Somente a afirmativa (I).
- Somente a afirmativa (II).
- Nenhuma das afirmativas.
- As afirmativas (I) e (II).
Passo 1
Vamos analisar cada uma das afirmativas. Comecemos pela afirmativa (I):
Se , então com certeza não é um máximo local de .
O que é necessário para que um ponto seja um ponto de máximo? É necessário que seja um ponto crítico, ou seja, que sua derivada tem que ser zero ou não pode existir.
O enunciado disse que a função é derivável, ou seja, a derivada sempre existe. Dessa maneira, resta que a derivada seja zero para que seja um ponto de máximo. Como , a derivada é diferente de zero, e, portanto, não pode ser ponto de máximo e a afirmação é verdadeira.
Passo 2
Vamos agora para a afirmativa (II):
- Se , então com certeza é um mínimo ou máximo local de .
Se , então é um ponto crítico. Se é um ponto crítico, então ele pode ser um ponto de máximo, mínimo ou nenhum dos dois. Quer um exemplo? Veja a função . Ela tem gráfico:
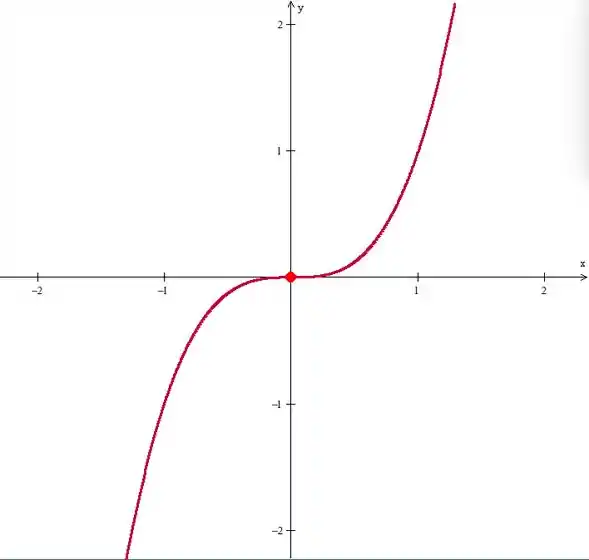
Derivando, temos:
No ponto , temos um ponto critico, pois a derivada é zero, mas é notório, pelo gráfico, que não se trata de um ponto de mínimo nem um ponto de máximo.
Portanto, a derivada ser zero não implica em pontos de máximos ou mínimos e a afirmação é falsa!
Assim sendo, a alternativa correta é a letra !
Resposta
letra !