Listas de Derivadas de Cálculo 1 da UFSC - Lista 2.1 - Tangente e Vel. Instantânea
Cálculo 1 - UFSC
2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtda. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
m.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
i.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
e.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
n.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
b.
Ver solução completa3. A posição (em metros) de um objeto em função do tempo (em segundos) é dada por . Determine a posição e a velocidade do objeto no instante .
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
m.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
h.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
l.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
d.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
k.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
f.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
c.
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
j.
Ver solução completa5. Determine uma equação para a reta que passa por e tem coeficiente linear igual a .
Ver solução completa- Em cada um dos itens abaixo, determine uma equação para a reta tangente ao gráfico da função no ponto de abscissa .
g.
Ver solução completa2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtida. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
h.
Ver solução completa2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtda. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtda. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
k.
Ver solução completa2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtda. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
j.
Ver solução completaC10) Refaça o item (c) do exercício C4 com uma função genérica e abscissas genéricas e .
Ver solução completaC2) Determine uma equação para a reta que passa por e tem coeficiente angular igual a .
Ver solução completaC3) Qual é o coeficiente angular da reta que passa pelos pontos e (assuma que ).
Ver solução completaC4) Considere a função .
b) Marque os pontos do gráfico de de abscissas e e desenhe a reta que passa por esses pontos.
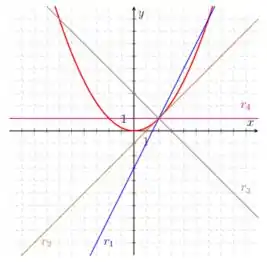
Ver solução completaC6) Na figura abaixo, há o gráfico da função e de quatro retas que passam pelo par ordenado . Qual dessas retas você escolheria para chamar de reta tangente ao gráfico de no ponto ?
C7) Entre as retas dos exercícios C4 e C5, qual é a mais parecida com a reta tangente escolhida no
exercício C6? O que mudou entre os exercícios C4 e C5 para que uma dessas retas fosse mais
parecida com a reta tangente? Como você faria para encontrar uma outra reta ainda mais parecida
com a reta tangente?
Ver solução completaC8) Por que, ao repetir o exercício C4 com abscissas repetidas 2 e 2, não obtemos como resposta a reta tangente ao gráfico de ?
Ver solução completaC9) Refaça o item (c) do exercício C4 com uma função genérica e abscissas genéricas e . Sugestão. Você já fez isso no exercício C3, basta observar que o ponto do gráfico de de abscissa qualquer é .
Ver solução completa