2. Para os itens e da questão anterior, faça o gráfico da função e da reta obtda. Verifique que, de fato, a reta obtida se comporta como uma reta tangente ao gráfico da função.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos que construir primeiro o gráfico da nossa que é
Galerinha, nós temos aqui uma função quadradica e a cara do gráfico desse tipo função é conhecida: ela é uma parábola.
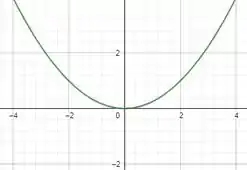
Agora vamos fazer o gráfico da reta tangente!
Passo 2
No exercício anterior , vimos que a equação da reta tangente é dada por:
E para traçarmos esse gráfico, basta achar os pontos onde e e depois traçar uma reta ligando eles. Fica assim:
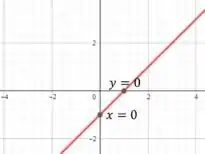
Passo 3
Juntando os dois gráficos, ficamos com:
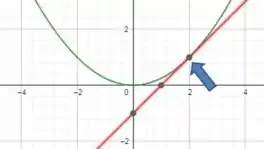
Note que os gráficos só se encontram no ponto .
Resposta
No texto.