UFSC; Cálculo 1; Lista 2.1 – Reta tangente e velocidade instantânea; Exercício C4a
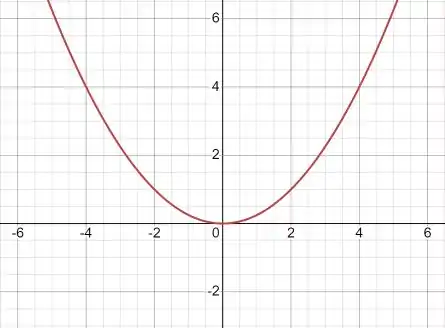
C4) Considere a função .
a) Faça o gráfico de .
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!
O primeiro passo desse exercício é esboçar o gráfico de . Precisamos, então, definir alguns pontos para esboçar .
O primeiro ponto que podemos encontrar é quando . Se :
Pontando é o vértice desse gráfico.
Como o número que acompanha é (positivo), então a concavidade dessa função de segundo grau será virada para cima.
Podemos definir dois pontos onde a parábola passa para desenharmos o gráfico.
Vamos utilizar e :
Então os pontos e fazem parte do gráfico.
Passo 2
Agora podemos desenhá-lo:
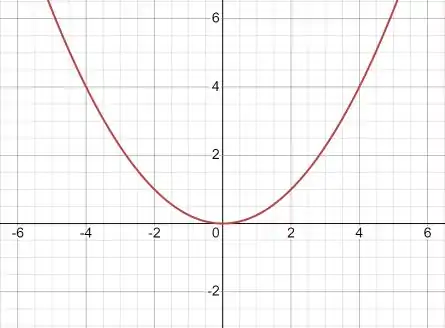
Ufa! Terminamos!
Pra essa questão é isso pessoal! Bora pra mais uma?
Resposta
Exercícios de Livros Relacionados
Encontre as equações da reta tangente e da reta normal à curva dada no ponto especificado: y = x x + 1 ,4 ,0.4
Encontre equações para areta tangente e para a reta normal à curva no ponto dado: y = 1 + 2 x 2 , ( 1 ,9 )
Encontre equações para a reta tangente e para a reta normal à curva no ponto especificado. y = 2 x e x ,0,0
Onde a reta normal à parábola y = x - x 2 no ponto 1,0 intercepta a parábola uma segunda vez? Ilustre com um esboço
23) Ache uma equação da reta tangente à curva y = 2 - 1 3 x 2 que é perpendicular à reta x - y = 0 .