C7) Entre as retas dos exercícios C4 e C5, qual é a mais parecida com a reta tangente escolhida no
exercício C6? O que mudou entre os exercícios C4 e C5 para que uma dessas retas fosse mais
parecida com a reta tangente? Como você faria para encontrar uma outra reta ainda mais parecida
com a reta tangente?
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!

Esse exercício é bem conceitual, onde precisamos decidir qual reta seria mais apropriada como uma reta tangente, a reta de C4 ou a reta de C5.
Mas o que é uma reta tangente a um ponto?
Reta tangente a um ponto de é uma reta que cruza por um e somente um ponto de . Ou seja, se a reta passa por dois pontos presentes em ela não é tangente.
Considerando esse conceito, vemos que a reta de C4 cruza em dois pontos e esses pontos são bem distantes entre si. Já na reta de C5, apesar de ainda cruzarmos em dois pontos, eles são bem próximos e, dependendo da escala de visualização do gráfico, parece ser um ponto apenas, veja:
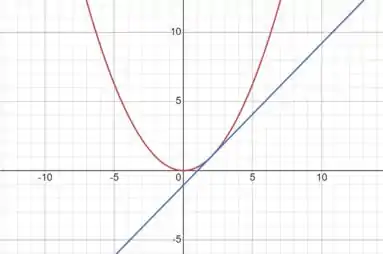
Portanto a reta de C5 seria mais indicada como reta tangente.
O que mudou entre C4 e C5 foi justamente a distância entre . Em C4 tínhamos e , já em C5 tínhamos e .
Para encontrar uma reta mais parecida ainda com a reta tangente, precisamos deixar as coordenadas de mais próximas ainda, como por exemplo e .
Ufa! Terminamos!

Pra essa questão é isso pessoal! Bora pra mais uma?
Resposta
Resolução nos Passos acima.