UFSC, Sem Campus, Cálculo 1, Listas de Derivadas - Lista 2.1 - Tangente e Vel. Instantânea, Questão C11
Usando as ideias dos exercícios , e ., explique de maneira informal por que o coeficiente angular da reta tangente ao gráfico de uma função no ponto de abscissa é
Passo 1
Eaew, tudo bem com você?
O enunciado nos indica como referência três exercícios , e , todos eles pedem para construirmos gráficos de uma função arbitrária em pontos específicos. Isto nos dá uma dica do procedimento para mostrarmos que o coeficiente angular da reta tangente é dado por
A melhor maneira de percebermos isso é analisar o sistema graficamente! Vamos lá!
Passo 2
Podemos imaginar uma função arbitrária que tenha uma gráfico qualquer como
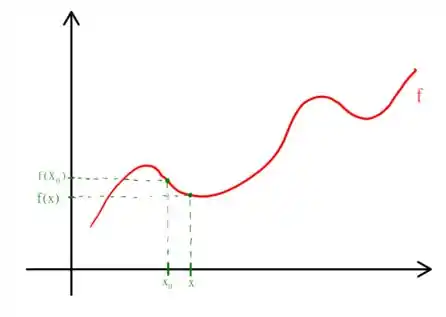
Note que indiquei que para e , como de se esperar em uma função usual! Mas como isso nos ajuda? Se traçarmos uma reta que cruza os dois pontos indicados, obtemos
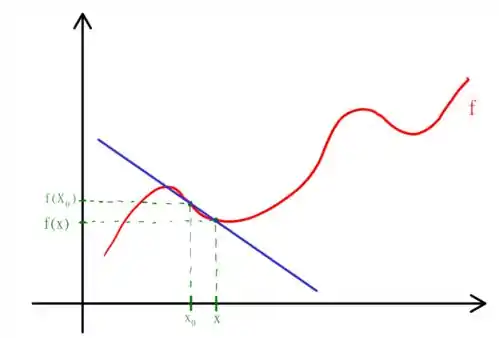
Note que esta reta azul não é tangente curva, mas se aproximarmos os pontos, ou seja, se fizermos que se aproxime de , e portanto, , a reta será tangente à curva no ponto . Okay, e como escrevemos isso matematicamente? Saca só!
Passo 3
Vamos dar um zoom em nosso esquema próximo aos dois pontos, temos que
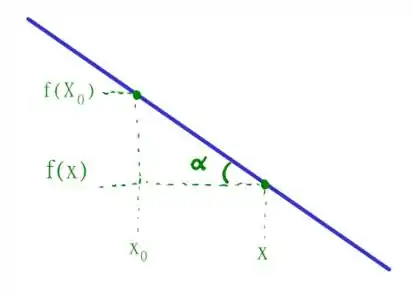
A definição geométrica de coeficiente angular é tal que
Observando o triângulo retângulo acima, temos podemos usar que
podemos identificar os nossos catetos através do esquema
O sinal negativo aparece simplesmente porque em meu esquema escolhi um referencial em que a inclinação da reta é negativa! Belezinha?
Passo 4
O que obtivemos anteriormente é o coeficiente angular de uma reta qualquer, para que seja a reta tangente, precisamos então aproximar o máximo que pudermos de , e portanto, temos que
Se usarmos a definição , podemos isolar tal que
e nestas condições quando , temos que , portanto, obtemos o seguinte limite
ou, equivalentemente, se escolhermos para montar o esquema, uma reta de inclinação positiva, temos
Como queríamos demonstrar! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!