P3 de Cálculo 1 da USP - 2019
Cálculo 1 - USP
Seja uma função contínua que satisfaz sendo uma constante não nula. O valor de é igual a:
- 4.
- 2.
- 1.
- 6.
- 0.
Seja uma função contínua que satisfaz sendo uma constante não nula. O valor de é igual a:
- 2.
- 4.
- 1.
- 6.
- 0.
Seja uma função contínua que satisfaz sendo uma constante não nula. O valor de é igual a:
- 2.
- 4.
- 1.
- 6.
- 0.
Seja uma função contínua que satisfaz sendo uma constante não nula. O valor de é igual a:
- 2.
- 4.
- 6.
- 0.
- 1.
Seja a região delimitada pelas curvas e e as retas e . O volume do sólido obtido pela rotação de em torno do eixo é:
Seja a região delimitada pelas curvas e e as retas e . O volume do sólido obtido pela rotação de em torno do eixo é:
Seja a região delimitada pelas curvas e e as retas e . O volume do sólido obtido pela rotação de em torno do eixo é:
Seja a região delimitada pelas curvas e e as retas e . O volume do sólido obtido pela rotação de em torno do eixo é:
Usando um polinômio de Taylor de ordem 2 ao redor de 1, a aproximação correta nas três primeiras casas decimais que obtemos para é:
a)
b)
c)
d)
e)
Ver solução completaUsando um polinômio de Taylor de ordem 2 ao redor de 1, a aproximação correta nas três primeiras casas decimais que obtemos para é:
a)
b)
c)
d)
e)
Ver solução completaUsando um polinômio de Taylor de ordem 2 ao redor de 1, a aproximação correta nas três primeiras casas decimais que obtemos para é:
a)
b)
c)
d)
e)
Ver solução completaUsando um polinômio de Taylor de ordem 2 ao redor de 1, a aproximação correta nas três primeiras casas decimais que obtemos para é:
a)
b)
c)
d)
e)
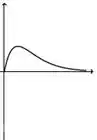
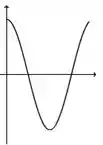
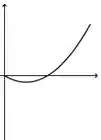
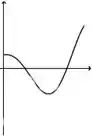
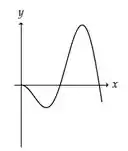
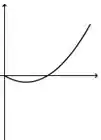
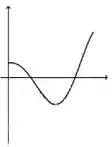
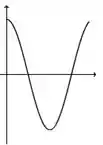
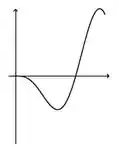
Ver solução completaA figura abaixo representa o gráfico de uma função .
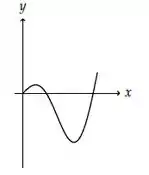
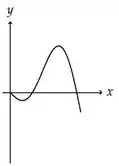
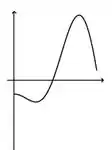
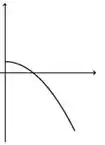
A figura que mais se aproxima do gráfico de uma primitiva de é:
a) 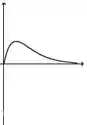
b) 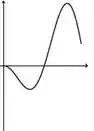
c) 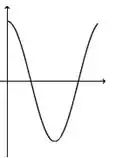
d) 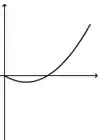
e)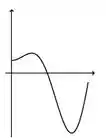
A figura abaixo representa o gráfico de uma função .
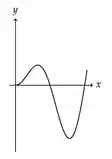
A figura que mais se aproxima do gráfico de uma primitiva de é:
a) 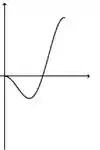
b) 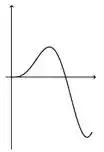
c) 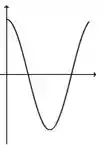
d) 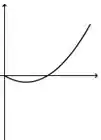
e)