O valor da integral
é:
a)
b)
c)
d)
e)
Passo 1
Uma propriedade de integral diz que a gente pode calcular a integral dessas funções e depois somar, assim:
Vamos avaliar como fica cada uma delas. Bora!
Passo 2
A primeira é essa:
Repara que o integrando dela é:
E aí a gente pode lembrar que é ímpar em relação à origem e também. E então, podemos supor que essa função do integrando que é composta por duas funções ímpares, também é ímpar.
Mas no que isso nos ajuda? Cara, quando a gente faz a integral de uma função ímpar sobre um intervalo simétrico em relação ao eixo , ou seja, que tem a forma , como o nosso tem :
Essa integral vai dar zero! Então a gente pode dizer que
Graficamente, isso é o que está acontecendo de uma forma geral
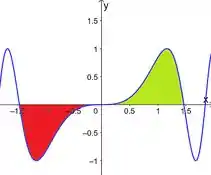
A gente tem do lado esquerdo uma área “negativa”, e do direito uma área “positiva”. Como elas tem a mesma dimensão, quando somamos elas, achamos um resultado nulo.
Passo 3
Vamos avaliar a segunda
A gente pode dizer que ela é a área entre a curva e o eixo . E isso no intervalo . Cara, isso é metade de cima de uma circunferência de raio .
Repara que podemos achar a equação da circunferência assim:
Se a gente quiser desenhar essa semicircunferência no intervalo , ficamos assim:
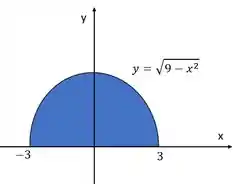
E daí a gente tira que nossa integral é a área desse semicírculo. Como :
Passo 4
Voltando para a nossa integral completinha:
Como
Resposta
Letra a