USP, Cálculo 1- P3- 2019.1, questão 12
A área da região delimitada pelas curvas e e as retas e é igual a:
Passo 1
Vamos ver essa área aqui, começando pelo gráfico:
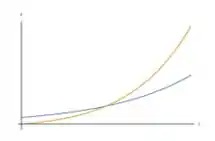
A gente quer a área a região representada no gráfico, mas pra isso a gente precisa saber qual função tá por cima e qual está por baixo.
Bom, vamos olhar no início do gráfico primeiro.
Para a função , se , temos o ponto .
Já para a função , se , temos o ponto .
Então daqui a gente descobre que a função em azul é e a função em laranja é .
Passo 2
Vamos ver agora onde é a interseção das duas curvas, igualando as duas:
Então, as curvas se encontram no ponto .
Observe que até esse ponto a função estava por cima e a partir dele a função é quem fica por cima.
A gente vai então dividir nossa região, já que queremos a área de .
Passo 3
A área pode ser dividida em:
Vamos chamar de :
A primeira parte da área é dada por:
Integrando, temos:
A primeira é imediata:
A segunda a gente vai usar integração por partes!
Passo 4
A gente quer resolver:
Vamos usar integração por partes, que é assim:
Vamos chamar de:
Então...
Aí substituindo ali em cima com os intervalos de integração:
Passo 5
Agora vamos fazer a outra parte da área:
Uhul! Agora falta pouquinho!
Passo 6
Show! Agora só falta somar as duas áreas:
Prontinho! Essa é a área pedida!
Alternativa D! 😊
Resposta
D)