P-SUB de Física 1 da USP - 2020

Q - Dois patinadores, de massas e , deslizam em linha reta sobre uma pista de gelo sem atrito, estando de mãos dadas. A velocidade dos patinadores é , enquanto eles andam de mão dadas. Num determinado instante eles se empurram e o patinador de massa passa a deslizar com velocidade e o

de massa passa a mover-se com velocidade . Nestas condições, a energia fornecida pelo

empurrão, em Joules, é:

• Considere os patinadores como partículas.

Q - Uma partícula de massa move-se em um plano horizontal . O vetor posição, que aponta da origem para a partícula, é dado por , com unidades no SI. Podemos afirmar que, no instante , o módulo do vetor torque em relação a origem , em , a que a partícula está sujeita é:

Q - Uma partícula de massa , que pode mover-se em um plano , inicialmente em repouso na posição , é sujeita à aceleração . Ao final de segundos, contados a partir do início do movimento, o módulo do momento angular da partícula em relação à origem do sistema de coordenadas, em , é:

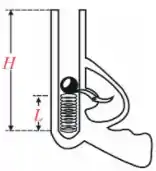
Q - Um revólver de brinquedo é usado para disparar projéteis de massa , verticalmente, utilizando para isso a compressão de uma mola de constante elástica e comprimento natural (não deformada) . Quando o revólver é preparado para atirar, a mola é comprimida e seu comprimento é . Desprezando

atritos e resistência com o ar, e sabendo que o comprimento interno do cano é , a

velocidade do projétil, em , quando sai do cano após o disparo é:

• Considere o projétil como uma partícula de massa .

Q - Durante o intervalo de tempo de a , uma partícula de massa experimenta uma mudança na sua velocidade de a , respectivamente, como consequência da ação da força resultante constante . Podemos afirmar que o valor do módulo da força , medido em Newtons, que

age na partícula, é:

Q - Uma partícula de massa (medida em ) se movimenta sob a ação da força resultante (medida em Newtons). Se em a partícula está localizada em (medido em metros) e tem velocidade (medida em ), determine o módulo do vetor posição da partícula (medido em metros) em um instante (medido em segundos).

Q - Uma partícula desloca-se em movimento retilíneo sobre o eixo . Sabe-se que no instante ela encontra-se em e sua velocidade em função do tempo é dada por

onde as unidades estão no SI. Podemos afirmar que no instante , sua posição, em metros, é:

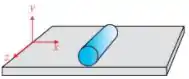
Q - Um cilindro de raio rola sem deslizar sobre uma superfície horizontal, como mostra a figura. Partindo do repouso , o cilindro inicia seu movimento com aceleração angular constante . A distância percorrida pelo centro de massa do cilindro desde o início do movimento até , em metros, é:

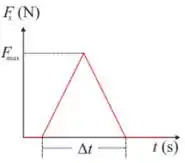
Q - Uma bola de tênis de e com velocidade inicial colide com uma parede e retorna com velocidade de mesmo valor em módulo. A figura abaixo representa a força da parede sobre a bola durante a colisão. Sabendo-se que o tempo que dura a colisão entre a bola e a parede é , o máximo valor da força que a parede exerce sobre a bola durante a colisão, em Newtons, é:

• Considere a bola como uma partícula de massa .

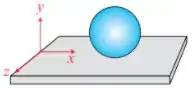
Q - Uma esfera oca de raio movimenta-se sobre uma superfície horizontal rugosa com velocidade e velocidade angular inicial . Após quanto tempo, em segundos, contado a partir do início do movimento, a esfera começa a rodar sem deslizar?

Q - Uma partícula desloca-se em movimento retilíneo sobre o eixo . Sabe-se que no instante ela encontra-se em e sua velocidade em função do tempo é dada por

onde as unidades estão no SI. Podemos afirmar que o deslocamento da partícula, em metros,

no intervalo é:

Q - Uma partícula desloca-se em movimento retilíneo sobre o eixo . Sabe-se que no instante ela encontra-se em e sua velocidade em função do tempo é dada por

onde as unidades estão no SI. Podemos afirmar que a distância percorrida pela partícula no intervalo é:

Q - Uma esfera oca de raio movimenta-se sobre uma superfície horizontal rugosa com velocidade e velocidade angular inicial . Após quanto tempo, em segundos, contado a partir do início do movimento, a esfera começa a rodar sem deslizar?

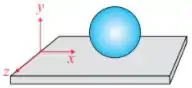
Q - Um sistema é formado por duas partículas de massas e presas às extremidades de uma barra rígida de massa desprezível. O sistema gira na ausência de atrito em um plano horizontal , em torno do ponto fixo , conforme mostra a figura. As distâncias das massas e em relação à são e , respectivamente. Se o módulo da velocidade da partícula de massa é , o módulo do momento angular do sistema em relação ao ponto , em , é:

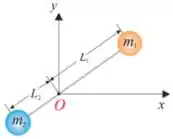
Q - Uma partícula de massa se movimenta com velocidade e colide elasticamente com uma partícula em repouso de massa como mostrado na figura. Após a colisão, é observado que as duas partículas têm mesma componente dos vetores velocidade. Determine o módulo do vetor velocidade da partícula de massa , em , imediatamente após a colisão.

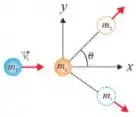
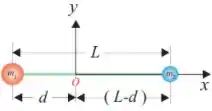
Q - Duas partículas pontuais de massas e estão conectadas por uma haste rígida (de massa desprezível) e comprimento podendo se movimentar no plano . O momento de inércia do sistema, em , em relação a um eixo perpendicular ao plano e que passa pelo centro de massa do sistema é:

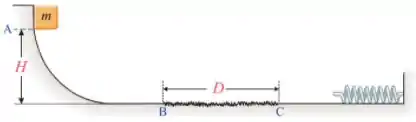
Q - Um bloco de massa é largado do ponto de uma altura , como mostra a figura abaixo. Ele percorre um caminho sem atrito até o ponto . Em seguida, ele atravessa uma região com atrito, apenas entre os pontos e , de comprimento , até colidir com uma mola de constante de força , comprimindo-a em , até parar. Podemos afirmar que o coeficiente de atrito existente na região entre os pontos e vale:

• Considere o bloco como uma partícula de massa .

Q - Um carro de massa deslocando-se em uma trajetória retilínea com velocidade colide com um muro de concreto que resiste ao impacto (não se

deforma). Por causa da colisão, o carro deforma-se e o centro de massa desloca-se a distância

, na direção do muro, com desaceleração constante. Podemos afirmar que o módulo da força média, em Newtons, exercida pelo muro sobre o carro é:

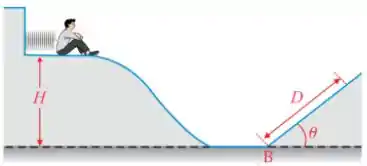
Q - Uma mola, de constante elástica , é usada, em um parque de diversões, para lançar pessoas em um escorregador de altura , como mostra a figura abaixo. A pista do escorregador não tem atrito desde o início (ponto de lançamento das

pessoas) até o ponto (começo da subida da rampa), onde o coeficiente de atrito passa a ser . A inclinação da rampa é tal que e . Se uma pessoa de massa for lançada quando a mola está comprimida em relação ao seu comprimento natural, a distância que ela percorrerá na rampa antes de parar, em metros, é:

• Considere a pessoa como uma partícula de massa .

Q - Em um certo referencial inercial, uma partícula, de massa movimentando-se com velocidade sobre uma superfície horizontal, colide elasticamente com uma partícula de massa que está parada. Considerando que o movimento das partículas após a colisão continua sendo ao longo do eixo , o módulo do vetor velocidade (em ) da partícula de massa imediatamente depois da colisão, no referencial centro de massa, é: