Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
USP – Física 1 – 2020 – P-SUB – Discursiva
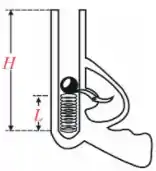
Q - Um revólver de brinquedo é usado para disparar projéteis de massa , verticalmente, utilizando para isso a compressão de uma mola de constante elástica e comprimento natural (não deformada) . Quando o revólver é preparado para atirar, a mola é comprimida e seu comprimento é . Desprezando
atritos e resistência com o ar, e sabendo que o comprimento interno do cano é , a
velocidade do projétil, em , quando sai do cano após o disparo é:
• Considere o projétil como uma partícula de massa .
Passo 1
Vem comigo que a gente detona com esse problema!
O enunciado pede a velocidade com que o projétil sai do revólver. Para encontrá-la podemos usar a conservação de energia mecânica ao nosso favor.
Vamos considerar o momento inicial quando a mola está comprimida, antes do revólver se disparado, nesse momento não temos energia cinética, só potencial gravitacional e elástica.
O momento final quando o projétil está na boca do revólver, nesse momento teremos energia cinética e energia potencial gravitacional.
Sabendo disso a conservação da energia fica da seguinte forma:
Para o cálculo da energia potencial, vamos considerar o zero de energia potencial na base do cano da arma, que é também a base inferior da mola.
Passo 2
A energia potencial gravitacional inicial é dada por:
A energia potencial elástica é dada por:
Onde , então:
Passo 3
A energia cinética final é dada por:
Onde é a velocidade que queremos saber.
A energia potencial gravitacional vai ser dada por:
Passo 4
Então a equação da conservação da energia mecânica que chegamos no passo fica da seguinte maneira:
Agora temos que isolar .
Logo, temos que:
Substituindo os valores que conhecemos, ficamos com:
Então, temos que:
Essa é a velocidade com que o projétil sai do revólver.