USP – Física 1 – 2020 – P-SUB – Discursiva
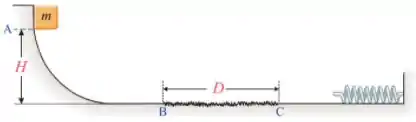
Q - Um bloco de massa é largado do ponto de uma altura , como mostra a figura abaixo. Ele percorre um caminho sem atrito até o ponto . Em seguida, ele atravessa uma região com atrito, apenas entre os pontos e , de comprimento , até colidir com uma mola de constante de força , comprimindo-a em , até parar. Podemos afirmar que o coeficiente de atrito existente na região entre os pontos e vale:
- Considere o bloco como uma partícula de massa .
Passo 1
Vem comigo que juntos a gente resolve essa questão!
O problema quer saber o coeficiente de atrito cinético no trecho . Olhando a situação vemos que o bloco parte do repouso, então sua energia cinética é zero e quando ele comprime a mola no final a sua velocidade é zero, logo sua energia cinética também, então:
Então todo esse percurso temos três forças que realizam trabalho no bloco, a força gravitacional, a de atrito e a elástica. Usando o teorema do trabalho/energia cinética, temos que:
Como a variação da energia cinética é zero, temos:
Vamos então encontrar expressões para esses trabalhos e extrair o coeficiente de atrito cinético.
Vamos nessa!
Passo 2
O trabalho é igual a força vezes a distância que essa força atuou. Começando com a força peso temos que:
A distância é , pois a força peso não depende da trajetória.
O trabalho da força de atrito é dado por:
Mas como no trecho o bloco está em repouso na vertical temos que , então:
Agora o trabalho da força elástica é dado por:
Onde é o deslocamento da mola.
Passo 3
Juntando tudo o que sabemos, ficamos com:
Agora vamos isolar .
Substituindo os valores que conhecemos, temos:
Então temos que:
Fechamos essa então!