USP – Física 1 – 2020 – P-SUB – Discursiva
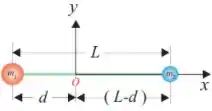
Q - Duas partículas pontuais de massas e estão conectadas por uma haste rígida (de massa desprezível) e comprimento podendo se movimentar no plano . O momento de inércia do sistema, em , em relação a um eixo perpendicular ao plano e que passa pelo centro de massa do sistema é:
Passo 1
Vem comigo que a gente resolve essa juntos.
O momento de inércia de partículas ligadas por uma haste em relação a um eixo é dado por:
Onde é a massa da partícula e é a distância entre a partícula e o eixo no qual queremos saber o momento de inercia.
Para o caso do nosso problema temos o eixo perpendicular que passa pelo centro de massa no qual queremos saber o momento de inércia está no ponto , logo:
Mas o enunciado não nos fornece o valor de , então temos que encontrar uma expressão para ele.
Passo 2
Para encontrar uma expressão para , vamos usar o fato de que o centro de massa se encontra na posição , então:
Passo 3
Conhecendo essa expressão para , vamos usar no momento de inércia, temos:
Com isso temos que:
Passo 4
Agora vamos substituir os valores que conhecemos, temos:
Logo temos que:
E fechamos essa questão com sucesso!