Q - Um sistema é formado por duas partículas de massas e presas às extremidades de uma barra rígida de massa desprezível. O sistema gira na ausência de atrito em um plano horizontal , em torno do ponto fixo , conforme mostra a figura. As distâncias das massas e em relação à são e , respectivamente. Se o módulo da velocidade da partícula de massa é , o módulo do momento angular do sistema em relação ao ponto , em , é:
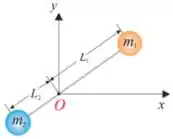
Passo 1
Vem comigo que a gente resolve essa juntos!
As partículas desenvolvem um movimento circular, então ambas têm a mesma velocidade angular, então o módulo do momento angular para essa situação é dado por:
Onde para o nosso caso temos:
Então temos que calcular o valor de e , para calcularmos o módulo do momento.
Passo 2
Temos que:
Mas como não temos o valor de , vamos usar a primeira igualdade. Temos então:
Passo 3
Agora vamos calcular , temos:
Substituindo o que sabemos, temos:
Assim temos que:
Passo 4
Agora podemos calcular o módulo do momento angular, temos:
Com isso temos que:
Pronto!! Tudo terminado!