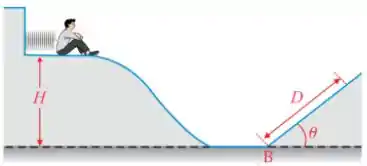
Q - Uma mola, de constante elástica , é usada, em um parque de diversões, para lançar pessoas em um escorregador de altura , como mostra a figura abaixo. A pista do escorregador não tem atrito desde o início (ponto de lançamento das
pessoas) até o ponto (começo da subida da rampa), onde o coeficiente de atrito passa a ser . A inclinação da rampa é tal que e . Se uma pessoa de massa for lançada quando a mola está comprimida em relação ao seu comprimento natural, a distância que ela percorrerá na rampa antes de parar, em metros, é:
• Considere a pessoa como uma partícula de massa .
Passo 1
Vamos juntos que a gente dá conta dessa questão!
Para encontrarmos podemos usar conservação de energia mecânica, mas o diferente é que temos o trabalho da força de atrito que atua na rampa (é uma força não conservativa), assim a conservação fica da seguinte forma:
No momento inicial como a pessoa parte do repouso, temos que a energia cinética inicial é zero, então só temos energia potencial gravitacional e elástica inicialmente.
Agora, no final quando a pessoa atinge a distância máxima na rampa a velocidade também é zero, logo só temos energia potencial gravitacional, com isso a conservação da energia mecânica fica assim:
Podemos desconsiderar a parte reta entre o escorrego e a rampa já que a energia cinética na base do escorrego é igual a energia na base da rampa, já que a velocidade não mudou, logo a variação é zero.
Vamos então atrás das energias potenciais inicial e final.
Passo 2
Vamos começar com a inicial, temos:
A energia potencial é dada por:
A elástica é dada por:
Com isso temos que:
Passo 3
Agora vamos ver a energia potencial final, temos que:
A energia potencial na rampa é dada por:
Onde , logo:
Passo 4
Por último temos que saber o trabalho da força de atrito na rampa, a força de atrito cinético é dada por:
Onde por conta da inclinação da rampa.
Então o trabalho dessa força em uma distância é dado por:
O trabalho é negativo já que a força de atrito é uma força dissipativa.
Passo 5
Juntando tudo o que temos, ficamos com:
Agora temos que isolar , já que queremos saber o valor desse cara.
Substituindo os valores que temos.
Com isso temos que:
Essa é a distância que a pessoa chega na rampa!