P1 de Física 1 da USP - 2020

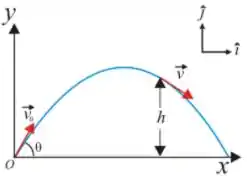
Q. Uma bola é lançada para o alto a partir da origem de um sistema cartesiano . A magnitude da velocidade inicial é e o ângulo de lançamento é . Quando a bola atinge a altura , como na figura, o vetor velocidade da bola é , com unidades no . Considerando a resistência do ar desprezível, a altura máxima alcançada pela bola, medida em metros, é:

Q - Uma partícula desloca-se sobre um círculo de raio com vetor velocidade que varia com o tempo segundo a equação onde . Podemos afirmar que quando a partícula encontra-se na posição angular , o módulo do vetor aceleração, em , é:

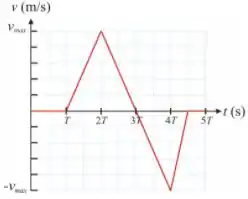
Q - O gráfico representa a velocidade em função do tempo de uma partícula que movimenta-se em uma trajetória retilínea. Sabe-se que no instante ela encontra-se na posição . Se , a posição da partícula no instante , medida em metros, é:

Q - Um corpo, partindo do repouso, percorre uma trajetória circular de raio , levando para completar a primeira volta. Sabendo que a aceleração angular é mantida constante, o intervalo de tempo (em segundos), a partir do início do movimento, gasto para percorrer um arco de comprimento igual a é:

Q - A trajetória de um projétil lançado do chão é dada pela equação

,

onde e são as coordenadas do projétil, medidas em metros. Se e , o módulo do vetor velocidade inicial do projétil, em metros por segundo, é:

Q - Uma partícula desloca-se no sentido anti-horário, sobre um círculo de raio com vetor velocidade que varia com o tempo segundo a equação (no SI). Sabe-se que em sua posição angular é . A posição angular da partícula no instante em que ela inverte o sentido do movimento, em radianos, é:

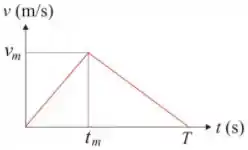
Q - Um carro, movimentando-se em uma trajetória retilínea, parte do repouso com aceleração , mantendo essa aceleração até o instante , quando a velocidade do carro atinge o valor . Após esse instante, o carro freia até parar em . Tal situação é representada no gráfico da velocidade do carro em função do tempo, como mostrado na figura. Sabendo-se que o carro percorreu uma distância até antes de parar, o tempo de duração da corrida , medido em segundos, é:

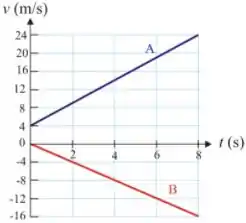
Q - Dois carros, e , deslocam-se em um longo trecho retilíneo de uma auto-estrada, em sentido contrário. No gráfico abaixo, estão representadas as velocidades dos automóveis e em função do tempo. Sabendo-se que os carros e se cruzam no instante , a distância entre eles, medida em metros, no instante de tempo , é:

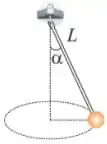
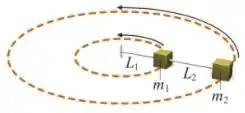
Q - Um bloco de massa está preso a um fio, de comprimento , que está fixo na outra extremidade. O bloco desloca-se num círculo horizontal, suportado por uma mesa sem atrito. Um segundo bloco, de massa , está ligado ao primeiro por um fio de comprimento e também se desloca num círculo, conforme mostrado na figura. Se os dois blocos giram com velocidade angular , a tensão no fio de comprimento , em Newtons, é:

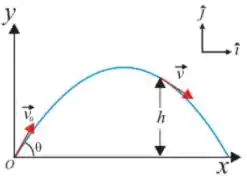
Q. Uma bola é lançada para o alto a partir da origem de um sistema cartesiano . A magnitude do vetor velocidade inicial é e o ângulo de lançamento é . Quando a bola atinge a altura , como na figura, o vetor velocidade da bola é , com unidades no . Considerando a resistência do ar desprezível, a distância horizontal no primeiro choque da bola com o solo, a partir da origem, medida em metros, é:

Q - A trajetória de um projétil lançado do chão é dada pela equação

,

onde e são as coordenadas do projétil, medidas em metros. Se o vetor velocidade de lançamento do projétil é , em unidades do SI, o valor do parâmetro , em unidades de , é

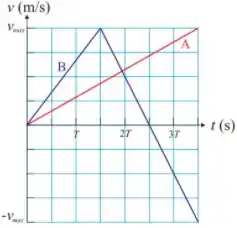
Q. Dois carros e , que estão inicialmente lado a lado, na mesma posição em uma pista retilínea, partem simultaneamente no instante . No gráfico abaixo, estão representadas as velocidades dos carros e como função do tempo. Se e , a distância entre os dois carros, no instante de tempo , medida em metros, é:

Q - O bloco de peso está preso a uma parede por meio de uma corda. Ele está colocado sobre o bloco que pesa e é puxado por uma força . O coeficiente de atrito nas superfícies inferior e superior do bloco é . O módulo da força necessária para arrastar o bloco com aceleração , mantendo-se o bloco em repouso, em Newtons, é:

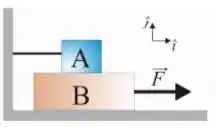
Q - A figura mostra um bloco de massa em repouso sobre um plano inclinado com inclinação . Ele está ligado a outro bloco, de massa , suspenso por meio de uma corda sem massa que passa por uma polia também desprovida de massa e livre de atrito. Os coeficientes de atrito estático e cinético com a superfície são respectivamente, e . Qual é o valor da massa , em kilogramas, para que o bloco de massa desça o plano inclinado com velocidade constante?

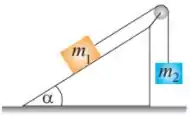
Q - A figura mostra um bloco de massa em repouso sobre um plano inclinado com inclinação . Ele está ligado a outro bloco, de massa , suspenso por meio de uma corda sem massa que passa por uma polia também desprovida de massa e livre de atrito. Os coeficientes de atrito estático e cinético com a superfície são, respectivamente, e . Qual é o valor da massa , em kilogramas, para que o bloco de massa suba o plano inclinado com velocidade constante?

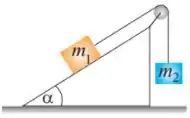
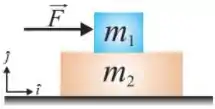
Q - Um bloco de massa é colocado sobre um bloco de massa , que encontra-se em repouso. Admitindo que os coeficientes de atrito estático e cinético entre os blocos são e , respectivamente, e que os coeficientes de atrito estático e cinético entre o bloco de massa e o solo são e , respectivamente, o

máximo valor de , em Newtons, que pode ser aplicada ao corpo de massa para que o sistema permaneça em repouso é:

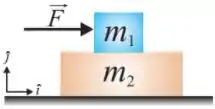
Q - A figura ao lado mostra dois blocos em contato, de massas e , que não estão fixados um ao outro. Uma força horizontal age no bloco de massa , como mostra a figura, fazendo com que eles andem juntos sobre uma superfície horizontal sem atrito. Se os coeficientes de atrito estático e cinético entre as superfícies de contato dos dois blocos valem respectivamente e , determine qual é o valor mínimo de necessário (expressado em Newtons) para que não deslize verticalmente em direção ao solo.

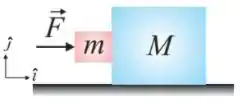
Q - Um bloco de massa é colocado sobre um bloco de massa , que encontra-se em repouso. Admita que os coeficientes de atrito estático e cinético entre os blocos são e , respectivamente, e que os coeficientes de atrito estático e cinético entre o bloco de massa e o solo são e , respectivamente. Netas condições, o máximo valor de , em Newtons, que aplicada ao corpo de massa movimenta o sistema sem que os blocos se desloquem relativamente um ao outro é:

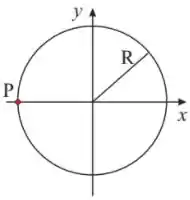
Q - Uma partícula percorre, em sentido horário, uma trajetória circular de raio , como na figura ao lado. Ao passar pelo ponto , mostrado na figura, o vetor aceleração total da partícula, em unidades do sistema internacional, é dado por

.

Considerando que a componente tangencial do vetor aceleração total seja constante, o módulo da velocidade da partícula segundo após ela passar pelo ponto P é:

Q - Uma partícula de massa está suspensa por uma corda de massa desprezível e comprimento . A extremidade superior da corda pode girar mantendo um ângulo com a vertical, como mostrado na figura. A partícula descreve um movimento circular. Determine o módulo do vetor velocidade da partícula (expresse o resultado em ). Despreze qualquer atrito e/ou arraste.