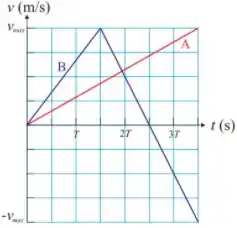
Q. Dois carros e , que estão inicialmente lado a lado, na mesma posição em uma pista retilínea, partem simultaneamente no instante . No gráfico abaixo, estão representadas as velocidades dos carros e como função do tempo. Se e , a distância entre os dois carros, no instante de tempo , medida em metros, é:
Passo 1
Vem comigo e não me abandona que a gente resolve essa questão!
O problema pede a distância entre os carros em , ele nos dá o gráfico das velocidades dos carros pelo tempo.
Então o que nós podemos fazer é calcular a área do gráfico de e , já que essa área fornece a variação de posição dos carros no intervalo de tempo .
Então temos que:
E
Mas segundo o enunciado os carros partem da mesma posição em , logo . Nós podemos considerar essa posição inicial igual a zero, já que ela não interfere em nada no cálculo, já que elas são iguais, com isso:
E
E a distância entre os carros em é dada por:
Vamos então encontrar essas áreas!
Passo 2
Começando com .
Olhando o gráfico vemos que o gráfico de é um triângulo com base e altura , assim:
Passo 3
Agora vamos ver a área de .
Esse gráfico é composto de dois triângulos, o primeiro com base e altura e o segundo com base e altura .
Então a área desse gráfico vai ser igual ao primeiro menos o segundo, da seguinte forma:
Passo 4
Com o que encontramos nos passos anteriores, temos que:
Então a distância entre os carros é dada por:
Usando que e , temos que:
E com isso finalizamos com sucesso!