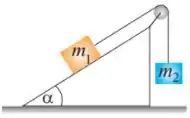
Q - A figura mostra um bloco de massa em repouso sobre um plano inclinado com inclinação . Ele está ligado a outro bloco, de massa , suspenso por meio de uma corda sem massa que passa por uma polia também desprovida de massa e livre de atrito. Os coeficientes de atrito estático e cinético com a superfície são, respectivamente, e . Qual é o valor da massa , em kilogramas, para que o bloco de massa suba o plano inclinado com velocidade constante?
Passo 1
Vem comigo que a gente derruba essa questão!
Primeiro vamos pensar no seguinte, para o bloco subir o plano com velocidade constante a força resultante na direção paralela a rampa deve ser zero.
E se o bloco sobe com velocidade constante o bloco desce com velocidade constante, logo a força resultante de na direção vertical deve ser zero.
Vamos ver o digrama de corpo livre desses blocos, assim fica mais claro as forças que atuam neles.
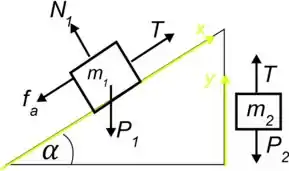
Agora vamos analisar o bloco na direção e o bloco na direção , lembrando que os dois devem ter velocidade constante, logo .
Passo 2
Vamos começar com , temos:
Usando que , temos:
A força de atrito é dada por:
Mas como , temos:
Passo 3
Agora vamos ver o bloco .
Então:
Passo 4
Como estamos em uma situação ideal, as tensões em cada bloco realizadas pela corda, são iguais, logo:
Então isolando , temos:
Agora substituindo os valores que temos, ficamos com:
Logo temos que:
Tá aí a massa que o problema pediu!