USP – Física 1 – 2020 – P1 – Discursiva
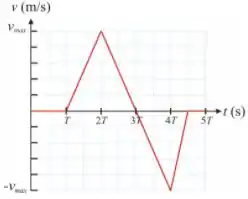
Q - O gráfico representa a velocidade em função do tempo de uma partícula que movimenta-se em uma trajetória retilínea. Sabe-se que no instante ela encontra-se na posição . Se , a posição da partícula no instante , medida em metros, é:
Passo 1
Vem comigo que juntos resolvemos essa questão!
O problema quer saber a posição no instante da partícula, para achar esse tempo vamos olhar o gráfico.
Temos um gráfico da velocidade pelo tempo e a área de gráficos desse tipo nos dão o deslocamento do corpo.
Sabendo disso, vamos considerar o intervalo de tempo , vamos escolher esse intervalo, já que o enunciado fornece a posição em então o deslocamento nesse intervalo de tempo é dado por:
Onde a área é a área da metade direta do triângulo de cima, com uma base e altura . A área é a área do triângulo de baixo, com uma base e altura .
Vamos as contas então!
Passo 2
A área é dada por:
A área é dada por:
Então temos que:
Assim:
Passo 3
Do passo , temos que:
Usando o que achamos no passo anterior, temos que:
Sabendo que em temos , logo:
Passo 4
Agora se assumirmos que , já que a um intervalo de temos dois quadradinhos no gráfico, ficamos com:
Prontinho, chegamos no que ele queria!