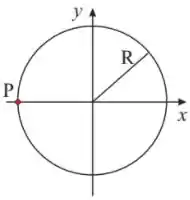
Q - Uma partícula percorre, em sentido horário, uma trajetória circular de raio , como na figura ao lado. Ao passar pelo ponto , mostrado na figura, o vetor aceleração total da partícula, em unidades do sistema internacional, é dado por

.

Considerando que a componente tangencial do vetor aceleração total seja constante, o módulo da velocidade da partícula segundo após ela passar pelo ponto P é:

Vem comigo que a gente detona nessa questão!

O que temos nessa situação é um movimento circular. Nesse tipo de movimento podemos ter duas acelerações, uma na direção tangencial a trajetória e uma na direção radial.

A aceleração radial pode ser calculada da seguinte forma:

Onde esse é a velocidade tangencial a trajetória da partícula. Então nesse problema só temos velocidade tangencial, já que o raio da trajetória não muda.

O problema nos dá o vetor aceleração no ponto . Onde é a aceleração radial e é a aceleração tangencial.

Já que temos o valor da aceleração radial, podemos encontrar a velocidade tangencial da partícula no ponto , tendo essa velocidade, podemos usar a seguinte equação da cinemática:

Onde é a velocidade no ponto , a aceleração tangencial, já que ela muda o módulo da velocidade tangencial e vai ser igual a que é onde ele quer saber o valor da velocidade .

Vamos nessa então!