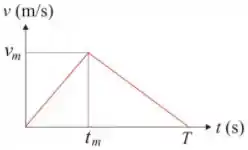
Q - Um carro, movimentando-se em uma trajetória retilínea, parte do repouso com aceleração , mantendo essa aceleração até o instante , quando a velocidade do carro atinge o valor . Após esse instante, o carro freia até parar em . Tal situação é representada no gráfico da velocidade do carro em função do tempo, como mostrado na figura. Sabendo-se que o carro percorreu uma distância até antes de parar, o tempo de duração da corrida , medido em segundos, é:
Passo 1
Vem comigo que a gente detona nessa questão!
O problema quer saber o tempo que que o carro leva para parar, para achar esse tempo vamos olhar o gráfico.
Temos um gráfico da velocidade pelo tempo e a área de gráficos desse tipo nos dão o deslocamento do corpo. O gráfico tem a forma de um triângulo com base e altura .
Assim o deslocamento do carro é igual a área desse gráfico. Vamos as contas.
Passo 2
Temos o seguinte:
área do triângulo
Isolando , temos:
O valor de já temos, flat encontrarmos .
Passo 3
Segundo o enunciado, o carro tem uma aceleração até o instante , então para achar podemos usar a equação da velocidade de um movimento acelerado, dada por:
Onde é a velocidade final que é igual a , a velocidade inicial que é zero (podemos ver no gráfico), assim temos eu:
Usando isso o tempo é dado por:
Passo 4
Agora vamos substituir os valores que conhecemos e achar .
Assim temos que:
Prontinho, tudo resolvido!