Q - O bloco de peso está preso a uma parede por meio de uma corda. Ele está colocado sobre o bloco que pesa e é puxado por uma força . O coeficiente de atrito nas superfícies inferior e superior do bloco é . O módulo da força necessária para arrastar o bloco com aceleração , mantendo-se o bloco em repouso, em Newtons, é:
Passo 1
Vem comigo que a gente vai detonar essa questão juntos!
Para podermos ver melhor o que está acontecendo, vamos montar um diagrama de corpo livre, temos o seguinte então:
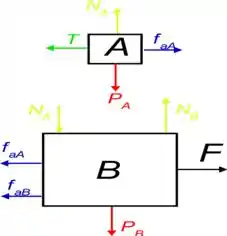
Onde as forças e são as forças normal e de atrito entre os blocos e as forças e são as forças da interação do bloco e o chão.
Como os blocos estão em repouso na direção , temos o seguinte:
Para o bloco :
Para o bloco :
Para que a força consiga puxar o bloco mantendo em repouso com uma aceleração de , teremos que ter uma força resultante na direção positivo com essa aceleração.
Usando a segunda lei de Newton para analisar o bloco , temos:
Onde , temos:
Então precisamos encontrar o valor das forças de atrito, para a gente conseguir isso vamos lembrar que a força de atrito é dada por:
Então para o nosso caso, teremos:
Vamos usar o coeficiente de atrito cinético pois estamos considerando o bloco em movimento tanto em relação ao chão quando em relação a .
Vamos as contas então!
Passo 2
Vamos calcular as forças de atrito de cada bloco.
Para o bloco , temos:
Como
ficamos com:
Para o bloco , temos:
Como
Já que , ficamos com:
Passo 3
Agora vamos substituir o que achamos na equação que chegamos no final do passo , temos:
O enunciado não nos deu a massa do bloco , mas ele nos deu o peso do bloco, então usando que:
Com isso ficamos com:
Agora vamos substituir os valores que conhecemos.
Então temos que:
E essa é o módulo da força que o enunciado pediu!