Q - Uma partícula de massa está suspensa por uma corda de massa desprezível e comprimento . A extremidade superior da corda pode girar mantendo um ângulo com a vertical, como mostrado na figura. A partícula descreve um movimento circular. Determine o módulo do vetor velocidade da partícula (expresse o resultado em ). Despreze qualquer atrito e/ou arraste.
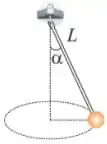
Passo 1
Vem comigo que a gente detona com essa questão.
Fazendo um diagrama de corpo livre da partícula, temos:
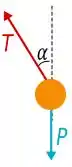
Olhando para o diagrama vemos que só temos duas forças atuando na partícula. Mas a força de tensão tem duas componentes, uma que aponta para o centro circunferência descrita pela partícula e uma apontando para cima .
Para essa partícula ter um movimento circular, ela precisa ter uma força resultante que aponte para o centro igual a força centrípeta, que é dada por:
Onde é o raio da trajetória circular feita pelo corpo.
O que o enunciado quer saber é justamente essa velocidade que aparece na expressão da força centrípeta.
Então vamos usar a segunda lei de Newton e analisar a partícula na direção e na direção (direção que aponta para o centro da trajetória circular)
Passo 2
Vamos lá, vamos começar com a direção , usando a segunda lei, temos:
Como , temos:
Passo 3
Agora vamos analisar a direção , temos que:
Como a corda que prende a partícula tem comprimento , o raio é igual a , assim temos que:
Substituindo a expressão para que encontramos no passo temos:
Essa seria a velocidade tangencial da partícula, a velocidade que aponta para a direção é zero já que o raio da circunferência é constante.
Então o módulo do vetor velocidade já que ele só tem uma componente é dado por: