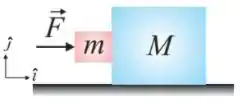
Q - A figura ao lado mostra dois blocos em contato, de massas e , que não estão fixados um ao outro. Uma força horizontal age no bloco de massa , como mostra a figura, fazendo com que eles andem juntos sobre uma superfície horizontal sem atrito. Se os coeficientes de atrito estático e cinético entre as superfícies de contato dos dois blocos valem respectivamente e , determine qual é o valor mínimo de necessário (expressado em Newtons) para que não deslize verticalmente em direção ao solo.
Passo 1
Vem comigo que a gente vence juntos!
Temos então que encontrar a força para que o bloco não deslize. Para conseguir chegar em um valor para essa força, temos que analisar as forças que temos em nosso problema. Vamos então fazer um diagrama de corpo livre. Ele fica da seguinte forma:

Olhando o diagrama podemos ver que para o bloco de massa não escorregue para baixo temos que ter a seguinte relação satisfeita:
Tanto , quanto e são constantes, então a única coisa que pode mudar é .
E o a força normal está ligada de alguma forma a força , já que ela faz com que o contato entre os blocos fique mais forte ou mais leve.
Vamos então usar a segunda lei de newton e avaliar esse sistema e ver o que conseguimos conectar.
Passo 2
Vamos aplicar a segunda lei Newton para o conjunto dos dois blocos na direção horizontal, temos o seguinte:
Temos então que:
Vamos deixar a aceleração isolada já que ela é iguala para os dois blocos.
Passo 3
Agora vamos usar a segunda lei só para o bloco , temos que:
Usando a expressão que encontramos para a aceleração, temos:
Então temos que:
Passo 4
Como vimos no passo para que o bloco não escorregue para baixo temos que:
Logo:
Então a força mínima para que o bloco não escorregue é quando as expressões são iguais, logo:
E com isso o bloco não escorrega kkk