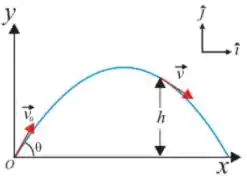
Q. Uma bola é lançada para o alto a partir da origem de um sistema cartesiano . A magnitude do vetor velocidade inicial é e o ângulo de lançamento é . Quando a bola atinge a altura , como na figura, o vetor velocidade da bola é , com unidades no . Considerando a resistência do ar desprezível, a distância horizontal no primeiro choque da bola com o solo, a partir da origem, medida em metros, é:
Passo 1
Vem comigo para gente resolver esse problema juntos!
Temos um caso de cinemática em duas direções, assim temos as seguintes informações para direção e .
Direção :
E para a direção , temos:
A partir delas vamos encontrar . Para isso vamos usar a terceira equação da direção , e como a bola parte da origem temos que , assim:
Mas como não temos aceleração em a velocidade é constante e pelo o que o enunciado deu sobre , temos que
Então só precisamos achar é o tempo que a bola leva até encostar no chão, que é igual ao tempo de subida da bola mais o de descida.
Passo 2
Para encontrar o tempo total, vamos primeiro descobrir a altura máxima que a bola atinge.
O enunciado nos diz que em uma altura a bola tem velocidade igual a na direção .
Se analisarmos o movimento que a bola faz partindo de até o chão, temos que a velocidade inicial , e já sabendo a velocidade em , podemos achar o tempo que a bola leva nesse percurso. Temos que:
Então a bola leva para percorrer uma distância entre o ponto e .
Passo 3
Sabendo o tempo que a bola leva para percorrer essa distância, podemos achar quanto ela vale. Vamos usar a equação da posição para direção , temos:
Sabendo que a posição é igual a , que é igual a , que a velocidade inicial é e que , temos:
Com isso temos que:
Essa é a altura máxima que a bola atinge.
Passo 4
Vamos então agora considerar o percurso de até o chão , usando a equação da posição na direção , temos:
Com isso temos que:
Esse é o tempo que a bola leva de até o chão (ou tempo de descida), então o tempo total (subidadescida) é o dobro disso, logo:
Passo 5
Agora podemos achar a distância percorrida pela bola, temos:
E com isso fechamos a questão!