Determine e esboce o domínio da função
Passo 1
Primeiramente vamos identificar e
Agora, quais são as restrições de cada uma delas?
Passo 2
Para temos uma raíz no denominador. Então sabemos que o que tem dentro da raiz tem que ser maior ou igual a zero, mas ao mesmo tempo tem que ser diferente de zero pois estão no denominador.
Assim
Passo 3
Para também temos uma raíz no denominador. Então sabemos que o que tem dentro da raiz tem que ser maior ou igual a zero, mas ao mesmo tempo tem que ser diferente de zero pois estão no denominador.
Assim
Então
Passo 4
A interseção dos dois domínios fica:
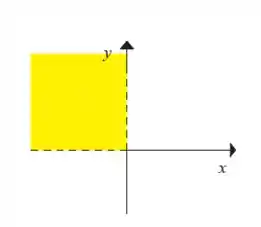
Graficamente teremos a parte do plano cartesiano em que é negativo e é positivo:
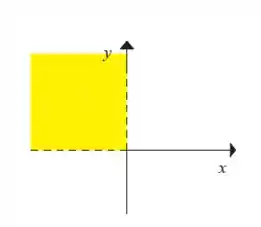
Resposta