UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 4ª Lista, Questão 1
01. Identifique a superfície representada pela equação .
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema foi dada uma superfície vetorial como e nosso objetivo é identificar a superfície formada por .
Tem ideia de como fazer isso? 🤔
Como nesse caso temos uma superfície vetorial de dimensões o que podemos fazer é definir e e substituir em , assim vamos encontrar no último termo do vetor uma função ...
Esboçando no espaço podemos identificar a superfície que é formada.
Sacou? Bora começar! 😉
Passo 2
Nossa superfície vetorial é dada por
Podemos perceber que a partir do primeiro e do segundo termo temos e .
O último termo é dado por
Mas se e , temos
Essa superfície é bem conhecida, não é? Trata-se de um paraboloide com a concavidade voltada para cima!
Esboçando a superfície no espaço, chegamos em
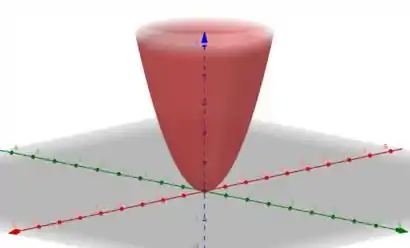
Sacou como faz? Responde Aí! 😉
Resposta
Um paraboloide.