Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mínimos Quadrados e Projeções

Ver Teoria
Exercício 512346789101112131415161718192021222324

Enunciado

A3 T15, A3 T14

Ajustando-se uma reta y = a x + b aos dados abaixo:

Obtêm-se os coeficientes a = 1.04 e b = - 0.0 8 . Use esta informação para calcular P H ⊥ ( 1.1 ,   1 . 8 ,   3 . 2 ,   3 . 8 ,   5 . 3 ) , a projeção ortogonal de ( 1.1 ,   1 . 8 ,   3 . 2 ,   3 . 8 ,   5 . 3 ) sobre o complemento ortogonal de H , onde

H = i m a g e m   d e   1 2 3 4 5 1 1 1 1 1 T

a   ( 0.14 ,   - 0.20 ,   0.16 ,   - 0.28 ,   0.18 )

b   ( 0 . 96 ,   2 . 00 ,   3 . 04 ,   4 . 08 ,   5 . 12 )

c   ( 0 . 912 ,   1 . 856 ,   2 . 744 ,   3 . 696 ,   4 . 576 )

d   ( 0 . 00 , - 0 . 33 ,   0 . 44 ,   0 . 11 , - 0 . 22 )

Passo 1

Repara o seguinte, com esses dados que ele deu pra gente, temos:

1 . x + b = 1.1 2 x + b = 1.8 3 x + b = 3.2 4 x + b = 3.8 5 x + b = 5.3

Passando isso pra forma matricial A x = b , temos:

A = 1 1 2 1 3 1 4 1 5 1

b = 1.1 1.8 3.2 3.8 5.3

E ele já deu o resultado de mínimos quadrados aplicado a isso:

1.04 - 0.08

Passo 2

Beleza, organizamos as informações que ele nos deu. Agora repara o seguinte! Temos que:

H = I m 1 1 2 1 3 1 4 1 5 1 = 1,2 , 3,4 , 5 , 1,1 , 1,1 , 1

Logo, nossa matriz A é a matriz cujas colunas são uma base de H ! Então se pegarmos o resultado dos mínimos quadrados e multiplicarmos por A teremos a projeção de b sobre H !

P H b = A z = 1 1 2 1 3 1 4 1 5 1 1.04 - 0.08 = 0.96 2 3.04 4.08 5.12

Passo 3

Eaí, acabou? Não né! Ele ta pedindo a projeção sobre o complemento ortogonal de H e não sobre H ! Mas aí é mole né? Lembra dessa imagem aqui?

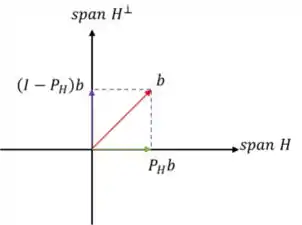
Repara que:

P H b + P H ⊥ b = b

P H ⊥ b = b - P H b

Show de bola! Temos b e temos a projeção dele em H já! Então é só subtrair:

P H ⊥ b = 1.1 1.8 3.2 3.8 5.3 - 0.96 2 3.04 4.08 5.12 = 0.14 - 0.2 0.16 - 0.28 0.18

Pronto! A resposta é a letra a !

Resposta

Letra ( a )

Exercícios de Livros Relacionados

1. Calcular o centróide dos vetores e representar geometricamente: u 1 = 1,2 e u 2 = 2,1 ; u 1 = 1,1 , u 2 = 1,2 , u 3 = 4 , - 1 e u 4 = 2,2 ; u 1 = 1,2 , 1 , u 2 = - 1 , - 2,0 e u 3 = 0,0 , - 1 ; u 1
3. Enunciar rigorosamente e provar: um operador linear do R n preserva os centróides.
4. Tomemos três vetores no R 2 , cujas extremidades formem um triângulo. Qual é o ponto do triângulo que coincide com a extremidade do centróide dos três vetores?
2. Seja u o centróide dos vetores u 1 , u 2 , … , u p do R n . Calcular nos exemplos do exercício 1 a soma u - u 1 2 + … + u - u p 2 .
Qual é a série de Fourier de s e n (3 x) ?