A3 T2 T17 T15
Seja o ponto do plano mais próximo de . A distância de a é:
Passo 1
Antes de sabermos a distância entre e , precisamos encontrar haha. Para isso, precisamos projetar. Vamos fazer o seguinte aqui, ao invés de usarmos a fórmula de mínimos quadrados direto, vou mostrar um caminho meio obscuro mas que vai ser bem mais rápido!
Ao invés de projetarmos sobre o plano, vamos projetar sobre a reta perpendicular que é dada pelo vetor:
Como estamos projetando em uma direção, podemos usar a fórmula do produto interno:
Agora lembra dessa imagem aqui:
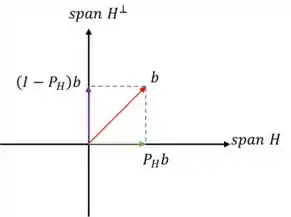
Repara que a distância entre , e sua projeção em , é justamente a projeção de sobre , que foi o que encontramos! Então agora só precisamos achar a norma disso.
Passo 2
Agora para acharmos a distância fazermos:
Resposta
Letra
Exercícios de Livros Relacionados
1. Calcular o centróide dos vetores e representar geometricamente: u 1 = 1,2 e u 2 = 2,1 ; u 1 = 1,1 , u 2 = 1,2 , u 3 = 4 , - 1 e u 4 = 2,2 ; u 1 = 1,2 , 1 , u 2 = - 1 , - 2,0 e u 3 = 0,0 , - 1 ; u 1
3. Enunciar rigorosamente e provar: um operador linear do R n preserva os centróides.
4. Tomemos três vetores no R 2 , cujas extremidades formem um triângulo. Qual é o ponto do triângulo que coincide com a extremidade do centróide dos três vetores?
2. Seja u o centróide dos vetores u 1 , u 2 , … , u p do R n . Calcular nos exemplos do exercício 1 a soma u - u 1 2 + … + u - u p 2 .
Qual é a série de Fourier de s e n (3 x) ?